【题目】已知三角形三边之长能求出三角形的面积吗？
海伦公式告诉你计算的方法是：S= ，其中S表示三角形的面积，a，b，c分别表示三边之长，p表示周长之半，即p= ．
我国宋代数学家秦九韶提出的“三斜求积术”与这个公式基本一致，所有这个公式也叫“海伦﹣秦九韶公式”．
请你利用公式解答下列问题．
（1）在△ABC中，已知AB=5，BC=6，CA=7，求△ABC的面积；
（2）计算（1）中△ABC的BC边上的高．

A. 21×10－5B. 2.1×10－7C. 2.1×10－5D. 2.1×10－6

A. 18a4b3B. －36a4b3C. －108a4b3D. 108a4b3

A. 8B. 6C. 4D. 2

如图①'在正方形ABCD中，过A点有直线AP，点B关于AP的对称点为E，连接DE交AP于点F,当∠BAP=20°时，则∠AFD= °；当∠BAP=α°(0<α<45°)时，则∠AFD= °；猜想线段DF, EF, AF之间的数量关系：DF-EF= AF（填系数）；

(2)数学思考：

如图②,若将“正方形ABCD中”改成“菱形ABCD中，∠BAD=120°”，其他条件不变，则∠AFD= °；线段DF, EF, AF之间的数量关系是否发生改变，若发生改变，请写出数量关系并说明理由；

(3)类比探究：

如图③，若将“正方形ABCD中”改成“菱形ABCD中，∠BAD=α°”，其他条件不变，则∠AFD= °；请直接写出线段DF,EF,AF之间的数量关系： .

【题目】如图，AB是⊙O的直径，且AB =6，C是⊙O上一点，D是的中点，过点D作⊙O的切线，与AB、AC的延长线分别交于点E、F，连接AD.

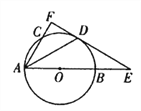
(l)求证：AF⊥EF;

(2)填空：

①当BE= 时，点C是AF的中点；

②当BE= 时，四边形OBDC是菱形，

【题目】AC是一棵大树，BF是一个斜坡，坡角为30°，某时刻太阳光垂直照射斜坡BF，树顶端A的影子落到斜坡上的点D处，已知BC=6m,BD=4m，求树AC的高度．（结果精确到0.1m．参考数据： ）

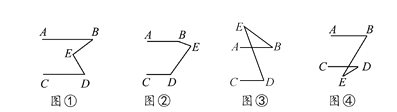
（1）你能探究出图①到图④各图中的∠B，∠D与∠BED之间的关系吗？

（2）请从所得的四个关系中，选一个说明它成立的理由．