
科目: 来源: 题型:
【题目】探究题
(1)【证法回顾】
证明:三角形中位线定理.
已知:如图1,DE是△ABC的中位线.
求证:DE∥BC,DE= ![]() BC.
BC.
证明:添加辅助线:如图1,在△ABC中,延长DE (D、E分别是AB、AC的中点)到点F,使得EF=DE,连接CF;请继续完成证明过程: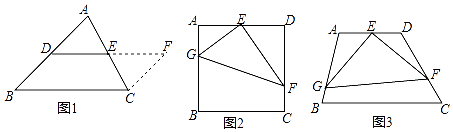
(2)【问题解决】
如图2,在正方形ABCD中,E为AD的中点,G、F分别为AB、CD边上的点,若AG=2,DF=3,∠GEF=90°,求GF的长.
(3)【拓展研究】如图3,在四边形ABCD中,∠A=105°,∠D=120°,E为AD的中点,G、F分别为AB、CD边上的点,若AG=3 ![]() ,DF=2,∠GEF=90°,求GF的长.
,DF=2,∠GEF=90°,求GF的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系中,把直线y=﹣2x+3沿y轴向上平移两个单位长度后,得到的直线的函数关系式为( )
A. y=﹣2x+1 B. y=﹣2x﹣5 C. y=﹣2x+5 D. y=﹣2x+7
查看答案和解析>>
科目: 来源: 题型:
【题目】一列快车从甲地开往乙地,一列慢车从乙地开往甲地,两车同时出发,两车离乙地的路程s(千米)与行驶时间t(小时)的关系如图所示,则下列结论中错误的是( )
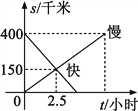
A. 甲、乙两地的路程是400千米 B. 慢车行驶速度为60千米/小时
C. 相遇时快车行驶了150千米 D. 快车出发后4小时到达乙地
查看答案和解析>>
科目: 来源: 题型:
【题目】如图①,在△ABC中,∠ACB=90°,AC=BC,过点C在△ABC外作直线MN,AM⊥MN于点M,BN⊥MN于点N.
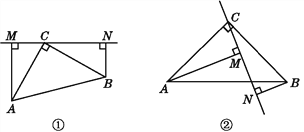
(1)试说明:MN=AM+BN.
(2)如图②,若过点C作直线MN与线段AB相交,AM⊥MN于点M,BN⊥MN于点N(AM>BN),(1)中的结论是否仍然成立?说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,抛物线y=x2+bx+c过点A(﹣4,﹣3),与y轴交于点B,对称轴是x=﹣3,请解答下列问题:
(1)求抛物线的解析式.
(2)若和x轴平行的直线与抛物线交于C,D两点,点C在对称轴左侧,且CD=8,求△BCD的面积.

查看答案和解析>>
科目: 来源: 题型:
【题目】 将抛物线y=x2-2x+1向下平移2个单位,再向左平移1个单位,所得抛物线的解析式是( )
A.y=x2-2x-1B.y=x2+2x-1C.y=x2-2D.y=x2+2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com