
科目: 来源: 题型:
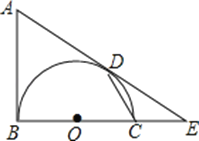
【题目】如图,AB是以BC为直径的半圆O的切线,D为半圆上一点,AD=AB,AD,BC的延长线相交于点E.
(1)求证:AD是半圆O的切线;
(2)连结CD,求证:∠A=2∠CDE;
(3)若∠CDE=30°,OB=2,求![]() 的长.
的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知矩形的面积为1,设该矩形的长为x,周长为y,小彬借鉴以前研究函数的经验,对函数y随自变量x的变化进行了探究;以下是小彬的探究过程:
(1)结合问题情境分析: ①y与x的函数表达式为;②自变量x的取值范围是 .
(2)下表是y与x的几组对应值.
x | … |
|
|
| 1 | 2 | 3 | 4 | … |
y | … |
|
| 5 | 4 | m |
|
| … |
①写出m的值;
②画出函数图象;
③观察图象,写出该函数两条不同类型的性质.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,从左到右,在每个小格子都填入一个整数,使得其中任意三个相邻格子中所填整数之和都相等.
|
|
|
|
|
|
|
(![]() )可求得
)可求得![]() __________.第
__________.第![]() 个格子中的数为__________.
个格子中的数为__________.
(![]() )判断:前
)判断:前![]() 个格子中所填整数之和是否可能为
个格子中所填整数之和是否可能为![]() ?若能,求出
?若能,求出![]() 的值;若不能,请说明理由.
的值;若不能,请说明理由.
(![]() )如果
)如果![]() 、
、![]() 为前三个格子中的任意两个数,那么所有的
为前三个格子中的任意两个数,那么所有的![]() 的和可以通过计算:
的和可以通过计算:
![]() 得到,若
得到,若![]() ,
, ![]() 为前
为前![]() 个格子中的任意两个数,则所有的
个格子中的任意两个数,则所有的![]() 的和为__________.
的和为__________.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在边长为8的正方形ABCD中,点O为AD上一动点(4<OA<8),以O为圆心,OA的长为半径的圆交边CD于点M,连接OM,过点M作⊙O的切线交边BC于N.
(1)求证:△ODM∽△MCN;
(2)设DM=x,OA=R,求R关于x的函数关系式;
(3)在动点O逐渐向点D运动(OA逐渐增大)的过程中,△CMN的周长如何变化?说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,△ABC为锐角三角形,AD是BC边上的高,正方形EFGH的一边FG在BC上,顶点E、H分别在AB、AC上,已知BC=40cm,AD=30cm.
(1)求证:△AEH∽△ABC;
(2)求这个正方形的边长.

查看答案和解析>>
科目: 来源: 题型:
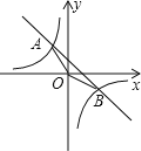
【题目】如图,已知一次函数y=kx+b的图象与反比例函数![]() 的图象交于A,B两点,且点A的横坐标和点B的纵坐标都是﹣2,
的图象交于A,B两点,且点A的横坐标和点B的纵坐标都是﹣2,
求:(1)一次函数的解析式;
(2)△AOB的面积;
(3)直接写出一次函数的函数值大于反比例函数的函数值时x的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知在Rt△ABC中,∠C=900,AD是∠BAC的角分线.
(1)以AB上的一点O为圆心,AD为弦在图中作出⊙O.(不写作法,保留作图痕迹);
(2)试判断直线BC与⊙O的位置关系,并证明你的结论;

查看答案和解析>>
科目: 来源: 题型:
【题目】已知:如图,AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E,∠BAC=45度.给出以下五个结论:①∠EBC=22.5°;②BD=DC;③AE=2EC;④劣弧AE是劣弧DE的2倍;⑤AE=BC.其中正确结论的序号是( )
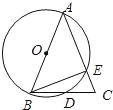
A. ①②③ B. ①②④ C. ①②⑤ D. ①②③⑤
查看答案和解析>>
科目: 来源: 题型:
【题目】![]() 年,德国数学家格奥尔格康托尔引入位于一条线段上的一些点的集合,他的做法如下:
年,德国数学家格奥尔格康托尔引入位于一条线段上的一些点的集合,他的做法如下:
取一条长度为![]() 的线段,将它三等分,去掉中间一段,余下两条线段,达到第
的线段,将它三等分,去掉中间一段,余下两条线段,达到第![]() 阶段;将剩下的两条线段再分别三等分.各去掉中间一段,余下四条线段,达到第
阶段;将剩下的两条线段再分别三等分.各去掉中间一段,余下四条线段,达到第![]() 阶段;再将剩下的四条线段,分别三等分,各去掉中间一段,余下八条线段,达到第
阶段;再将剩下的四条线段,分别三等分,各去掉中间一段,余下八条线段,达到第![]() 线段;
线段; ![]() ;这样的操作一直继续下去,在不断分割舍弃的过程中,所形成的线段数目越来越多,把这种分形,称做康托尔点集.下图是康托尔点集的最初几个阶段,当达到
;这样的操作一直继续下去,在不断分割舍弃的过程中,所形成的线段数目越来越多,把这种分形,称做康托尔点集.下图是康托尔点集的最初几个阶段,当达到![]() 个阶段时(
个阶段时(![]() 为正整数),的线段的长度之和为__________.
为正整数),的线段的长度之和为__________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com