
科目: 来源: 题型:
【题目】如图(1),在平面直角坐标系中,点A、C分别在y轴和x轴上,AB∥x轴,cosB=![]() .点P从B点出发,以1cm/s的速度沿边BA匀速运动,点Q从点A出发,沿线段AO-OC-CB匀速运动.点P与点Q同时出发,其中一点到达终点,另一点也随之停止运动.设点P运动的时间为t(s),△BPQ的面积为S(cm2), 已知S与t之间的函数关系如图(2)中的曲线段OE、线段EF与曲线段FG.
.点P从B点出发,以1cm/s的速度沿边BA匀速运动,点Q从点A出发,沿线段AO-OC-CB匀速运动.点P与点Q同时出发,其中一点到达终点,另一点也随之停止运动.设点P运动的时间为t(s),△BPQ的面积为S(cm2), 已知S与t之间的函数关系如图(2)中的曲线段OE、线段EF与曲线段FG.
(1)点Q的运动速度为 cm/s,点B的坐标为 ;
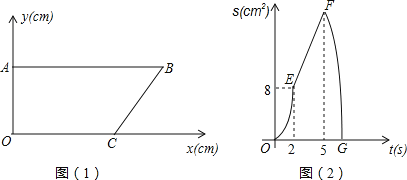
(2)求曲线FG段的函数解析式;
(3)当t为何值时,△BPQ的面积是四边形OABC的面积的![]() ?
?
查看答案和解析>>
科目: 来源: 题型:
【题目】“知识改变命运,科技繁荣祖国.”为提升中小学生的科技素养,我区每年都要举办中小学科技节.为迎接比赛,某校进行了宣传动员并公布了相关项目如下:
A——杆身橡筋动力模型;B——直升橡筋动力模型;C——空轿橡筋动力模型.右图为该校报名参加科技比赛的学生人数统计图.
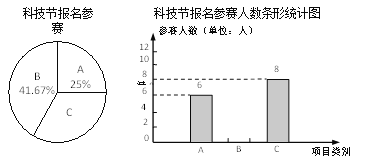
(1)该校报名参加B项目学生人数是 人;
(2)该校报名参加C项目学生人数所在扇形的圆心角的度数是 °;
(3)为确定参加区科技节的学 生人选,该校在集训后进行了校内选拔赛,最后一轮复赛,决定在甲、乙2名候选人中选出1人代表学校参加区科技节B项目的比赛,每人进行了4次试飞,对照一定的标准,判分如下:甲:80,70,100,50;乙:75,80,75,70.如果你是教练,请你用学过的数学统计量分析派谁代表学校参赛?请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某公司准备投资开发A、B两种新产品,信息部通过调研得到两条信息:
信息一:如果投资A种产品,所获利润![]() (万元)与投资金额x(万元)之间满足正比例函数关系:
(万元)与投资金额x(万元)之间满足正比例函数关系: ![]() ;
;
信息二:如果投资B种产品,所获利润![]() (万元)与投资金额x(万元)之间满足二次函数关系:
(万元)与投资金额x(万元)之间满足二次函数关系: ![]() ;
;
根据公司信息部报告, ![]() 、
、![]() (万元)与投资金额x(万元)的部分对应值如下表所示:
(万元)与投资金额x(万元)的部分对应值如下表所示:
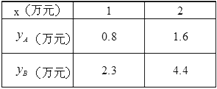
(1)填空: ![]() = ;
= ; ![]() = ;
= ;
(2)如果公司准备投资20万元同时开发A、B两种新产品,设公司所获得的总利润为W(万元),B种产品的投资金额为x(万元),则A种产品的投资金额为_________万元,并求出W与x之间的函数关系式;
(3)请你设计一个在(2)中公司能获得最大总利润的投资方案.
查看答案和解析>>
科目: 来源: 题型:
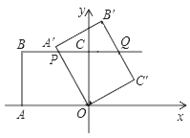
【题目】如图,在平面直角坐标系中,O为坐标原点,点A的坐标为(-8,0),直线BC经过点B(-8,6),C(0,6),将四边形OABC绕点O按顺时针方向旋转α度(0<α ≤180°)得到四边形OA′B′C′,此时直线OA′、直线B′C′分别与直线BC相交于P、Q.在四边形OABC旋转过程中,若BP=![]() BQ,则点P的坐标为__________.
BQ,则点P的坐标为__________.
查看答案和解析>>
科目: 来源: 题型:
【题目】探索函数![]() 的图象和性质.
的图象和性质.
已知函数y=x(x>0)和![]() 的图象如图所示,若P为函数
的图象如图所示,若P为函数![]() 图象上的点,过P作PC垂直于x轴且与直线、双曲线、x轴分别交于点A、B、C,则PC=
图象上的点,过P作PC垂直于x轴且与直线、双曲线、x轴分别交于点A、B、C,则PC= ![]() =AC+BC,从而“点P可以看作点A的沿竖直方向向上平移BC个长度单位(PA=BC)而得到”.
=AC+BC,从而“点P可以看作点A的沿竖直方向向上平移BC个长度单位(PA=BC)而得到”.
(1)根据以上结论,请在下图中作出函数![]() 图象上的一些点,并画出该函数的图象.
图象上的一些点,并画出该函数的图象.
(2)观察图象,写出函数![]() 两条不同类型的性质.
两条不同类型的性质.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,△ABE是等腰三角形,AB=AE,∠BAE=45°,过点B作BC⊥AE于点C,在BC上截取CD=CE,连接AD、DE并延长AD交BE于点P; 
(1)求证:AD=BE;
(2)试说明AD平分∠BAE;
(3)如图2,将△CDE绕着点C旋转一定的角度,那么AD与BE的位置关系是否发生变化,说明理由. 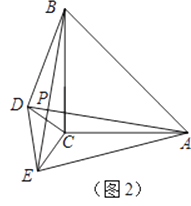
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com