
科目: 来源: 题型:
【题目】在数学探究课上,老师出示了这样的探究问题,请你一起来探究:
已知:C是线段AB所在平面内任意一点,分别以AC,BC为边,在AB同侧作等边三角形ACE和BCD,联结AD,BE交于点P.
(1)如图1,当点C在线段AB上移动时,线段AD与BE的数量关系是: . 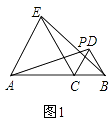
(2)如图2,当点C在直线AB外,且∠ACB<120°,上面的结论是否还成立?若成立请证明,不成立说明理由.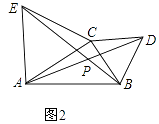
(3)在(2)的条件下,∠APE的大小是否随着∠ACB的大小的变化而发生变化,若变化,写出变化规律,若不变,请求出∠APE的度数.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,点P为∠AOB内一点,分别作出点P关于OA、OB的对称点P1、P2 , 连接P1P2交OA于M,交OB于N,若P1P2=6,则△PMN的周长为 . 
查看答案和解析>>
科目: 来源: 题型:
【题目】下列等式从左到右的变形,属于因式分解的是( )
A.8x2 y3=2x24 y3B.( x+1)( x﹣1)=x2﹣1
C.3x﹣3y﹣1=3( x﹣y)﹣1D.x2﹣8x+16=( x﹣4)2
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,点A在第一象限,点P在x轴上,若以P,O,A为顶点的三角形是等腰三角形,则满足条件的点P共有( )
A.2个
B.3个
C.4个
D.5个
查看答案和解析>>
科目: 来源: 题型:
【题目】(1)问题背景
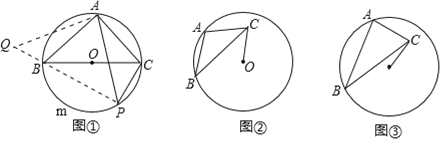
如图①,BC是⊙O的直径,点A在⊙O上,AB=AC,P为BmC上一动点(不与B,C重合),求证: ![]() PA=PB+PC.
PA=PB+PC.
小明同学观察到图中自点A出发有三条线段AB,AP,AC,且AB=AC,这就为旋转作了铺垫.于是,小明同学有如下思考过程:
第一步:将△PAC绕着点A顺时针旋转90°至△QAB(如图①);
第二步:证明Q,B,P三点共线,进而原题得证.
请你根据小明同学的思考过程完成证明过程.
(2)类比迁移
如图②,⊙O的半径为3,点A,B在⊙O上,C为⊙O内一点,AB=AC,AB⊥AC,垂足为A,求OC的最小值.
(3)拓展延伸
如图③,⊙O的半径为3,点A,B在⊙O上,C为⊙O内一点,AB=![]() AC,AB⊥AC,垂足为A,则OC的最小值为 .
AC,AB⊥AC,垂足为A,则OC的最小值为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com