练习册

  • 练习册
  • 试题
    相关习题
     0  344884  344892  344898  344902  344908  344910  344914  344920  344922  344928  344934  344938  344940  344944  344950  344952  344958  344962  344964  344968  344970  344974  344976  344978  344979  344980  344982  344983  344984  344986  344988  344992  344994  344998  345000  345004  345010  345012  345018  345022  345024  345028  345034  345040  345042  345048  345052  345054  345060  345064  345070  345078  366461 

    科目： 来源： 题型：

    【题目】如图，△ABC中，AD平分∠BAC，DG⊥BC且平分BC，DE⊥AB于E，DF⊥AC于F．

    （1）求证：BE=CF；

    （2）如果AB=8，AC=6，求AE、BE的长．

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】阅读资料：小明是一个爱动脑筋的好学生，他在学习了有关圆的切线性质后，意犹未尽，又查阅到了与圆的切线相关的一个问题：

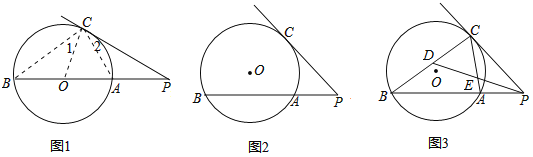
    如图1，已知PC是⊙O的切线，AB是⊙O的直径，延长BA交切线PC与P，连接AC、BC、OC．

    因为PC是⊙O的切线，AB是⊙O的直径，所以∠OCP=∠ACB=90°，所以∠1=∠2．
    又因为∠B=∠1，所以∠B=∠2．

    在△PAC与△PCB中，又因为：∠P=∠P，所以△PAC∽△PCB，所以，即PC2=PAPB．

    问题拓展：

    （Ⅰ）如果PB不经过⊙O的圆心O（如图2）等式PC2=PAPB，还成立吗？请证明你的结论；

    综合应用：

    （Ⅱ）如图3，⊙O是△ABC的外接圆，PC是⊙O的切线，C是切点，BA的延长线交PC于点P；

    （1）当AB=PA，且PC=12时，求PA的值；

    （2）D是BC的中点，PD交AC于点E．求证：．

    　

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】如图：在△ABC中，∠C=90°,AD是∠BAC的平分线，DE⊥AB于E，F在AC上，BD=DF；

    证明：（1）CF=EB．

    （2）AB=AF+2EB．

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】已知x1，x2，x3，x4的方差是a，则3x1﹣5，3x2﹣5，3x3﹣5，3x4﹣5的方差是__．

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】线段AB两端点A(－1，2)，B(4，2)，则线段AB上任意一点可表示为___________．

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】如图，等边△ABC的边长为6，∠ABC，∠ACB的角平分线交于点D，过点D作EF∥BC，交AB、CD于点E、F，则EF的长度为___________．

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】已知等腰三角形的两边长分别为2和5，则该等腰三角形的周长为（ ）

    A.7B.9C.9或12D.12

    查看答案和解析>>

    科目： 来源： 题型：

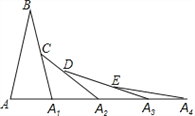
    【题目】如图，已知AB=A1B，A1C=A1A2，A2D=A2A3，A3E=A3A4，∠B=20°，则∠A4=（　　）

    A. 10° B. 15° C. 30° D. 40°

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】下列各式中，不能应用平方差公式进行计算的是（ ）

    A.（-x+2y）（2y+x）B.（x+y）（x-y）C.（a-b）（-a+b）D.（-2m+n）（-2m-n）

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】如图，⊙O是以原点为圆心，为半径的圆，点P是直线y=﹣x+6上的一点，过点P作⊙O的一条切线PQ，Q为切点，则切线长PQ的最小值为______.

    查看答案和解析>>

    同步练习册答案