
科目: 来源: 题型:
【题目】已知等边△ABC中,点D为射线BA上一点,作DE=DC,交直线BC于点E,∠ABC的平分线BF交CD于点F,过点A作AH⊥CD于H,当EDC=30![]() ,CF=
,CF=![]() ,则DH=______.
,则DH=______.

查看答案和解析>>
科目: 来源: 题型:
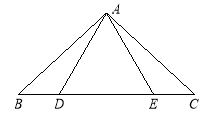
【题目】如图,点D,E在△ABC的边BC上,连 接AD,AE.①AB=AC;②AD=AE;③BD=CE.以此三个等式中的两个作为命题的题设,另一个作为命题的结论,构成三个命题:①②③:①③②;②③①.
(1)以上三个命题是真命题的为(直接作答) ;
(2)请选择一个真命题进行证明(先写出所选命题,然后证明)
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读材料:
我们经常通过认识一个事物的局部或其特殊类型,来逐步认识这个事物;比如我们通过学习特殊的四边形,即平行四边形(继续学习它们的特殊类型如矩形、菱形等)来逐步认识四边形;

我们对课本里特殊四边形的学习,一般先学习图形的定义,再探索发现其性质和判定方法,然后通过解决简单的问题巩固所学知识;
请解决以下问题:
如图,我们把满足AB=AD、CB=CD且AB≠BC的四边形ABCD叫做“筝形”;
⑴写出筝形的两个性质(定义除外);
⑵写出筝形的两个判定方法(定义除外),并选出一个进行证明.

查看答案和解析>>
科目: 来源: 题型:
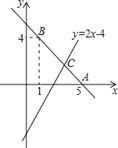
【题目】已知直线y=kx+b经过点A(5,0),B(1,4).
(1)求直线AB的解析式;
(2)若直线y=2x﹣4与直线AB相交于点C,求点C的坐标;
(3)根据图象,写出关于x的不等式2x﹣4>kx+b的解集.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,已知O是坐标原点,点A的坐标是(5,0),点B是y轴正半轴上一动点,以OB,OA为边作矩形OBCA,点E,H分别在边BC和边OA上,将△BOE沿着OE对折,使点B落在OC上的F点处,将△ACH沿着CH对折,是点A落在OC上的G点处。
(1)求证:四边形OECH是平行四边形;
(2)如图2,当点B运动到使得点F,G重合时,判断四边形OECH的形状并说明理由;
(3)当点B运动到使得点F,G将对角线OC三等分时,求点B的坐标。

查看答案和解析>>
科目: 来源: 题型:
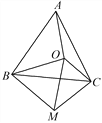
【题目】如图,点O为等边三角形ABC内一点,连接OA,OB,OC,以OB为一边作∠OBM=60°,且BO=BM,连接CM,OM.
(1)判断AO与CM的大小关系并证明;
(2)若OA=8,OC=6,OB=10,判断△OMC的形状并证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com