A.6B.12C.±6D.±12

【题目】资料：小球沿直线撞击水平格档反弹时（不考虑垂直撞击），撞击路线与水平格档所成的锐角等于反弹路线与水平格档所成的锐角．以图（1）为例，如果黑球 沿从 到 方向在 点处撞击 边后将沿从 到 方向反弹，根据反弹原则可知 ，即 ．如图（2）和（3）， 是一个长方形的弹子球台面，有黑白两球 和 ，小球沿直线撞击各边反弹时遵循资料中的反弹原则．（回答以下问题时将黑白两球均看作几何图形中的点，不考虑其半径大小）

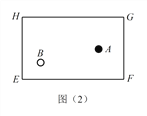
(1)探究（1）：黑球 沿直线撞击台边 哪一点时，可以使黑球 经台边 反弹一次后撞击到白球 ?请在图（2）中画出黑球 的路线图，标出撞击点，并简单证明所作路线是否符合反弹原则.

(2)探究（2）：黑球 沿直线撞击台边 哪一点时，可以使黑球 先撞击台边 反弹一次后，再撞击台边 反弹一次撞击到白球 ?请在图（3）中画出黑球 的路线图，标出黑球撞击 边的撞击点，简单说明作法，不用证明．

A. 逐渐减小 B. 逐渐增大 C. 先增大后减小 D. 先减小后增大

（1）当圆心O在∠BAD内部，∠ABO+∠ADO=60°时，∠BOD= ；

（2）当圆心O在∠BAD内部，四边形OBCD为平行四边形时，求∠A的度数；

（3）当圆心O在∠BAD外部，四边形OBCD为平行四边形时，请直接写出∠ABO与∠ADO的数量关系．

问题：已知方程x2+x﹣1=0，求一个一元二次方程，使它的根分别是已知方程根的2倍．

解：设所求方程的根为y，则y=2x，所以x=，把x=，代入已知方程，

得（）2 +﹣1=0．

化简，得y2+2y﹣4=0，

故所求方程为y2+2y﹣4=0

这种利用方程根的代换求新方程的方法，我们称为“换根法”．

请用阅读材料提供的“换根法”求新方程（要求：把所求方程化为一般形式）：

（1）已知方程x2+2x﹣1=0，求一个一元二次方程，使它的根分别是已知方程根的相反数，则所求方程为 ；

（2）已知关于x的一元二次方程ax2+bx+c=0（a≠0）有两个不等于零的实数根，求一个一元二次方程，使它的根分别是已知方程根的倒数．

A. （3，4） B. （﹣3，4） C. （﹣4，﹣3） D. （﹣3，﹣4）

【题目】如图，两条互相平行的河岸，在河岸一边测得AB为20米，在另一边测得CD为70米，用测角器测得∠ACD=30°，测得∠BDC=45°，求两条河岸之间的距离．（， ≈1.7，结果保留整数）