练习册

  • 练习册
  • 试题
    相关习题
     0  356849  356857  356863  356867  356873  356875  356879  356885  356887  356893  356899  356903  356905  356909  356915  356917  356923  356927  356929  356933  356935  356939  356941  356943  356944  356945  356947  356948  356949  356951  356953  356957  356959  356963  356965  356969  356975  356977  356983  356987  356989  356993  356999  357005  357007  357013  357017  357019  357025  357029  357035  357043  366461 

    科目： 来源： 题型：

    【题目】如图：

    （1）写出A、B、C三点的坐标；

    （2）若△ABC各顶点的横坐标不变，纵坐标都乘以﹣1，请你在同一坐标系中描出对应的点A′、B′、C′，并依次连接这三个点，所得的△A′B′C′与原△ABC有怎样的位置关系；

    （3）在②的基础上，纵坐标都不变，横坐标都乘以﹣1，在同一坐标系中描出对应的点A″、B″、C″，并依次连接这三个点，所得的△A″B″C″与原△ABC有怎样的位置关系．

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】如图，在△ABC中，∠C＝90°，∠A，∠B的平分线交于点D，DE⊥BC于点E，DF⊥AC于点F．

    ⑴ 求证：四边形CFDE是正方形； ⑵ 若AC＝3，BC＝4，求△ABC的内切圆半径．

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】如图，点C在以AB为半径的半圆上，AB＝8，∠CBA＝30°，点D在线段AB上运动，点E与点D

    关AC对称，DF⊥DE于点D，并交EC的延长线与点F．下列结论：①CE＝CF；②线段EF的最小值为2

    ③当AD＝2时，EF与半圆相切；④当点D从点A运动到点B时，线段EF扫过的面积是16．其中正

    确的结论（）

    A. 1个 B. 2个 C. 3个 D. 4个

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】如图，AB为⊙O的直径，CD切⊙O于点D，AC⊥CD交⊙O于点E，若∠BAC＝60°，AB＝4，则阴影部分的面积是（）

    A. B. C. D.

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】已知M(x，y)是平面直角坐标系xOy中的点，其中x是从l、2、3三个数中任取的一个数，y是从l、2、3、4四个数中任取的一个数 .

    (l)计算由x、y确定的点M(x，y)在函数y= -x+5的图象上的概率；

    (2)小明和小红约定做一个游戏，其规则为：若x、y满足xy＞6则小明胜；若x、y满足xy＜6则小红胜，这个游戏公平吗？说明理由. 若不公平，请写出公平的游戏规则；

    (3)定义“点M(x，y)在直线x+y=n上”为事件A(2≤n≤7，n为整数)，则当A的概率最大时，n的所有可能的值为 .（不需要解答过程）

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】在平面直角坐标系中，规定把一个三角形先沿x轴翻折，再向右平移两个单位称为一次变换，如图，已知等边三角形ABC的顶点B、C的坐标分别是，（-1，-1），（-3，-1），把三角形ABC经过连续9次这样的变换得到三角形A’B’C’，则点A的对应点A’的坐标是_____

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】正方形ABCD的边长为4，E为BC边上一点，BE=3，M为线段AE上一点，射线BM交正方形的一边于点F，且BF=AE,则BM的长为____．

    查看答案和解析>>

    科目： 来源： 题型：

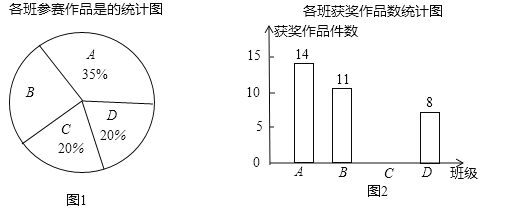
    【题目】【本小题满分9分】某校组织了一次初三科技小制作比赛，有A、B、C、D四个班共提供了100件参赛作品．C班提供的参赛作品的获奖率为50%，其他几个班的参赛作品情况及获奖情况绘制在下列图①和图②两幅尚不完整的统计图中．

    （1）B班参赛作品有多少件？

    （2）请你将图②的统计图补充完整；

    （3）通过计算说明，哪个班的获奖率高？

    （4）将写有A、B、C、D四个字母的完全相同的卡片放人箱中，从中一次随机抽出两张卡片，求抽到A、B两班的概率．

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】商店只有雪碧、可乐、果汁、奶汁四种饮料，每种饮料数量充足，某同学去该店购买饮料，每种饮料被选中的可能性相同．

    （1）若他去买一瓶饮料，则他买到奶汁的概率是 ；

    （2）若他两次去买饮料，每次买一瓶，且两次所买饮料品种不同，请用树状图或列表法求出他恰好买到雪碧和奶汁的概率．

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】（1）甲、乙、丙、丁四人做传球游戏：第一次由甲将球随机传给乙、丙、丁中的某一人，从第二次起，每一次都由持球者将球再随机传给其他三人中的某一人．求第二次传球后球回到甲手里的概率．（请用“画树状图”的方式给出分析过程）

    （2）如果甲跟另外n（n≥2）个人做（1）中同样的游戏，那么，第三次传球后球回到甲手里的概率是 （请直接写出结果）．

    查看答案和解析>>

    同步练习册答案