
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx﹣2与x轴交于点A、B(点A在点B的左侧),与y轴交于点C(0,﹣2),OB=4OA,tan∠BCO=2.
(1)求A、B两点的坐标;
(2)求抛物线的解析式;
(3)点M、N分别是线段BC、AB上的动点,点M从点B出发以每秒![]() 个单位的速度向点C运动,同时点N从点A出发以每秒2个单位的速度向点B运动,当点M、N中的一点到达终点时,两点同时停止运动.过点M作MP⊥x轴于点E,交抛物线于点P.设点M、点N的运动时间为t(s),当t为多少时,△PNE是等腰三角形?
个单位的速度向点C运动,同时点N从点A出发以每秒2个单位的速度向点B运动,当点M、N中的一点到达终点时,两点同时停止运动.过点M作MP⊥x轴于点E,交抛物线于点P.设点M、点N的运动时间为t(s),当t为多少时,△PNE是等腰三角形?

查看答案和解析>>
科目: 来源: 题型:
【题目】小明骑自行车上学,开始以正常速度匀速行驶,但行至中途时,自行车出了故障,只好停下来修车,车修好后,因怕耽误上课,他比修车前加快了速度继续匀速行驶,下面是行驶路程s(m)关于时间t(min)的函数图象,那么符合小明行驶情况的大致图象是()
A.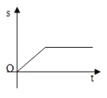 B.
B.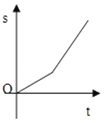 C.
C. D.
D.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,C为线段BD上一动点,分别过点B、D作AB⊥BD,ED⊥BD,连接AC、EC.已知AB=2,DE=1,BD=8,设CD=x.
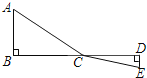
(1)用含x的代数式表示AC+CE的长;
(2)请问点C满足什么条件时,AC+CE的值最小;
(3)根据(2)中的规律和结论,请构图求出代数式![]() 的最小值.
的最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,∠B=90°,点P从点A开始沿AB边向点B以1㎝/秒的速度移动,同时点Q从点B开始沿BC边向点C以2㎝/秒的速度移动.(![]() )
)
(1)如果ts秒时,PQ//AC,请计算t的值.
(2)如果ts秒时,△PBQ的面积等于S㎝2,用含t的代数式表示S.
(3)PQ能否平分△ABC的周长?如果能,请计算出t值,不能,说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,AB=BC,以AB为直径的⊙O交BC于点D,交AC于点F,过点C作CE∥AB,与过点A的切线相交于点E,连接AD.
(1)求证:AD=AE;
(2)若AB=6,AC=4,求AE的长.

查看答案和解析>>
科目: 来源: 题型:
【题目】已知一角的两边与另一个角的两边平行,分别结合下图,试探索这两个角之间的关系,并证明你的结论.
(1)如图(1)AB∥EF,BC∥DE,∠1与∠2的关系是:____________ .

(2)如图(2)AB∥EF,BC∥DE, ∠1与∠2的关系是:____________

(3)经过上述证明,我们可以得到一个真命题:如果____ _____,那么____________.
(4)若两个角的两边互相平行,且一个角比另一个角的2倍少30°,则这两个角分别是多少度?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,点A,C的坐标分别为(a,0),(0,b),点B在第一象限内,且a,b满足|a3﹣64|+![]() =0.点P从原点出发,以每秒2个单位长度的速度沿着长方形OABC的边逆时针移动一周(即:沿着O→A→B→C→O的路线移动).
=0.点P从原点出发,以每秒2个单位长度的速度沿着长方形OABC的边逆时针移动一周(即:沿着O→A→B→C→O的路线移动).

(1)求点B的坐标;
(2)当点P移动4秒时,求出点P的坐标;
(3)在移动过程中,当点P到x轴的距离为5个单位长度时,请直接写出点P移动的时间t.
查看答案和解析>>
科目: 来源: 题型:
【题目】为了保护环境,某企业决定购买10台污水处理设备,现有A、B两种型号的设备,其中每台价格,月处理污水量极消耗费如下表:

经预算,该企业购买设备的资金不高于105万元.
⑴ 请你为企业设计几种购买方案.
⑵ 若企业每月产生污水2040吨,为了节约资金,应选那种方案?
查看答案和解析>>
科目: 来源: 题型:
【题目】在一次课外活动中,甲、乙两位同学测量公园中孔子塑像的高度,他们分别在A,B两处用高度为1.5m的测角仪测得塑像顶部C的仰角分别为30°,45°,两人间的水平距离AB为10m,求塑像的高度CF.(结果保留根号)

查看答案和解析>>
科目: 来源: 题型:
【题目】小明想利用太阳光测量楼高,他带着皮尺来到一栋楼下,发现对面墙上有这栋楼的影子,针对这种情况,他设计了一种测量方案,具体测量情况如下:如示意图,小明边移动边观察,发现站到点E处时,可以使自己落在墙上的影子与这栋楼落在墙上的影子重叠,且高度恰好相同.此时,测得小明落在墙上的影子高度CD=1.2m,CE=0.8m,CA=30m(点A、E、C在同一直线上).已知小明的身高EF是1.7m,请你帮小明求出楼高AB(结果精确到0.1m).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com