
科目: 来源: 题型:
【题目】如图所示,在平面直角坐标系中,已知A(2,2)、B(﹣2,0)、C(﹣1,﹣2).

(1)在平面直角坐标系中画出△ABC;
(2)若点D与点C关于y轴对称,则点D的坐标为 ;
(3)求△ABC的面积;
(4)已知点P为x轴上一点,若S△ABP=5时,求点P的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读下列材料:
情形展示:
情形一:如图![]() ,在
,在![]() 中,沿等腰三角形ABC的顶角
中,沿等腰三角形ABC的顶角![]() 的平分线
的平分线![]() 折叠,若点B与点C重合,则称
折叠,若点B与点C重合,则称![]() 是
是![]() 的“好角”,如图
的“好角”,如图![]() ,在
,在![]() 中,先沿
中,先沿![]() 的平分线
的平分线![]() 折叠,剪掉重复部分,再将余下部分沿
折叠,剪掉重复部分,再将余下部分沿![]() 的平分线
的平分线![]() 折叠,若点
折叠,若点![]() 与点C重合,则称
与点C重合,则称![]() 是
是![]() 的“好角”.
的“好角”.
情形二:如图![]() ,在
,在![]() 中,先沿
中,先沿![]() 的平分线
的平分线![]() 折叠,剪掉重复部分,再将余下部分沿
折叠,剪掉重复部分,再将余下部分沿![]() 的平分线
的平分线![]() 折叠,剪掉重复部分
折叠,剪掉重复部分![]() 重复折叠n次,最终若点
重复折叠n次,最终若点![]() 与点C重合,则称
与点C重合,则称![]() 是
是![]() 的“好角”,探究发现:
的“好角”,探究发现:![]() 不妨设
不妨设![]()
![]() 如图
如图![]() ,若
,若![]() 是
是![]() 的“好角”,则
的“好角”,则![]() 与
与![]() 的数量关系是:______.
的数量关系是:______.
![]() 如图
如图![]() ,若
,若![]() 是
是![]() 的“好角”,则
的“好角”,则![]() 与
与![]() 的数量关系是:______.
的数量关系是:______.
![]() 如图
如图![]() ,若
,若![]() 是
是![]() 的“好角”,则
的“好角”,则![]() 与
与![]() 的数量关系是:______.
的数量关系是:______.
应用提升:
![]() 如果一个三角形的三个角分别为
如果一个三角形的三个角分别为![]() ,
,![]() ,
,![]() ,我们发现
,我们发现![]() 和
和![]() 的两个角都是此三角形的“好角”;如果有一个三角形,它的三个角均是此三角形的“好角”,且已知最小的角是
的两个角都是此三角形的“好角”;如果有一个三角形,它的三个角均是此三角形的“好角”,且已知最小的角是![]() ,求另外两个角的度数.
,求另外两个角的度数.



查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC 中,点 D、E 分别在 BC、AC 上且 BD=CE,AD=DE, ∠C =∠ADE, 则∠B =∠C,试填写说理过程.

解因为∠EDB =∠C+∠DEC( )
即∠ADB+∠ADE =∠C+∠DEC
因为∠C =∠ADE( )
所以∠ =∠ (等式性质)
在△ABD 与△DCE 中,

所以△ABD ≌ △DCE( )
所以∠B =∠C( )
查看答案和解析>>
科目: 来源: 题型:
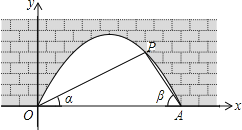
【题目】图中是抛物线拱桥,P处有一照明灯,点P到水面OA的距离为![]() ,从O、A两处观测P处,仰角分别为
,从O、A两处观测P处,仰角分别为![]() ,
,![]() ,且
,且![]() ,
,![]() ,以O为原点,OA所在直线为x轴建立直角坐标系,已知抛物线方程为
,以O为原点,OA所在直线为x轴建立直角坐标系,已知抛物线方程为![]() .
.
![]() 求抛物线方程,并求抛物线上的最高点到水面的距离;
求抛物线方程,并求抛物线上的最高点到水面的距离;
![]() 水面上升1m,水面宽多少
水面上升1m,水面宽多少![]() 取
取![]() ,结果精确到
,结果精确到![]() ?
?
查看答案和解析>>
科目: 来源: 题型:
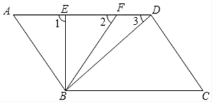
【题目】如图,已知AD∥BC,∠A=∠C=50°,线段AD上从左到右依次有两点E、F(不与A、D重合)
(1)AB与CD是什么位置关系,并说明理由;
(2)观察比较∠1、∠2、∠3的大小,并说明你的结论的正确性;
(3)若∠FBD:∠CBD=1:4,BE平分∠ABF,且∠1=∠BDC,求∠FBD的度数,判断BE与AD是何种位置关系?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,正方形ABCD中,点E,F分别在边,AD,CD上,且![]() ,BD和EF交于点O,延长BD至点H,使得
,BD和EF交于点O,延长BD至点H,使得![]() ,并连接HE,HF.
,并连接HE,HF.
![]() 求证:
求证:![]() ;
;
![]() 试判断四边形BEHF是什么特殊的四边形,并说明理由.
试判断四边形BEHF是什么特殊的四边形,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com