A. 20° B. 25° C. 30° D. 45°

【题目】反比例函数y=的图象向右平移个单位长度得到一个新的函数，当自变量x取1，2，3，4，5，…，（正整数）时，新的函数值分别为y1，y2，y3，y4，y5，…，其中最小值和最大值分别为（　　）

A. y1，y2 B. y43，y44 C. y44，y45 D. y2014，y2015

（课堂提问）王老师在课堂中提出这样的问题：如图1，在Rt△ABC中，∠ACB=90°，∠BAC=30°，那么BC和AB有怎样的数量关系？

（互动生成）经小组合作交流后，各小组派代表发言.

（1）小华代表第3小组发言：AB=2BC. 请你补全小华的证明过程.

证明：把△ABC沿着AC翻折，得到△ADC.

∴∠ACD=∠ACB=90°，

∴∠BCD=∠ACD+∠ACB=90°+90°=180°，

即：点B、C、D共线.

（请在下面补全小华的证明过程）

（2）受到第3小组“翻折”的启发，小明代表第2小组发言：如图2，在△ABC中，如果把条件“∠ACB=90°”改为“∠ACB=135°”，保持“∠BAC=30°”不变，若BC=1，求AB的长.

（能力迁移）我们发现，翻折可以探索图形性质，请利用翻折解决下面问题.

如图3，点D是△ABC内一点，AD=AC，∠BAD=∠CAD=20°，∠ADB+∠ACB=210°，则AD、DB、BC三者之间的数量关系是 .

（课后拓展）如图4，在四边形ABCD中，∠BCD=45°，∠BAD=90°，∠ADB=∠CDB=60°，且AC=1，

则△ABD的周长为 .

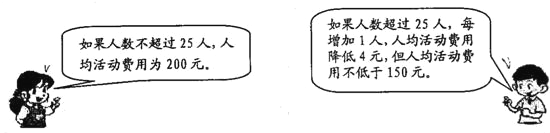
活动结束后，该班共支付给该旅行社活动费用5600元，该班共有多少人参加这次活动？

（1）求证：CB=CE；

（2）如图2，当点D运动到OA的中点时，CD刚好平分，求证：△BCE是等边三角形；

（3）如图3，当点D运动到与点O重合时，若⊙O的半径为2，且∠DCB=45°，求线段EF的长．

（1）当点C和点A重合时，求OM的长；

（2）若S△ACB=10，则t的值为 ；

（3）在（2）的条件下，直线AM交y轴于点N，求△ABN的面积.

（1）根据题意，填写下表：

（2）设甲，乙两人与A地的距离为y1（km）和y2（km），写出y1，y2关于x的函数解析式；

（3）设甲，乙两人之间的距离为y，当y=12时，求x的值．