
科目: 来源: 题型:
【题目】已知:在△ABC中,∠ACB=90°,点P是线段AC上一点,过点A作AB的垂线,交BP的延长线于点M,MN⊥AC于点N,PQ⊥AB于点Q,AQ=MN. 求证:
(1)△APM是等腰三角形;
(2)PC=AN.

查看答案和解析>>
科目: 来源: 题型:
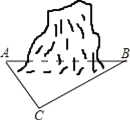
【题目】为促进我市经济的快速发展,加快道路建设,某高速公路建设工程中需修隧道AB,如图,在山外一点C测得BC距离为200m,∠CAB=54°,∠CBA=30°,求隧道AB的长.(参考数据:sin54°≈0.81,cos54°≈0.59,tan54°≈1.38, ![]() ≈1.73,精确到个位)
≈1.73,精确到个位)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,等边三角形ABC的边长为4,AD是BC边上的中线,F是AD边上的动点,E是AC边上一点.若AE=2,当EF+CF取得最小值时,∠ECF的度数为( )

A. 20° B. 25° C. 30° D. 45°
查看答案和解析>>
科目: 来源: 题型:
【题目】网瘾低龄化问题已经引起社会各界的高度关注,有关部门在全国范围内对12﹣35岁的网瘾人群进行了简单的随机抽样调查,绘制出以下两幅统计图.

请根据图中的信息,回答下列问题:
(1)这次抽样调查中共调查了 人;
(2)请补全条形统计图;
(3)扇形统计图中18﹣23岁部分的圆心角的度数是 ;
(4)据报道,目前我国12﹣35岁网瘾人数约为2000万,请估计其中12﹣23岁的人数
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,放置的△OAB1,△B1A1B2,△B2A2B3,…都是边长为2的等边三角形,边AO在y轴上,点B1、B2、B3…都在直线y=![]() x上,则点A2018的坐标为( )
x上,则点A2018的坐标为( )

A. (2018![]() ,2020) B. (2018
,2020) B. (2018![]() ,2018) C. (2020
,2018) C. (2020![]() ,2020) D. (2018,2020)
,2020) D. (2018,2020)
查看答案和解析>>
科目: 来源: 题型:
【题目】(1)如图①,在锐角△ABC中,BD和BE三等分∠ABC,CD和CE三等分∠ACB,请分别写出∠A和∠D,∠A和∠E的数量关系,并选择其中一个说明理由;
(2)如图②,在锐角△ABC中,BD和BE三等分∠ABC,CD和CE三等分外角∠ACM,请分别写出∠A和∠D,∠A和∠E的数量关系,并选择其中一个说明理由;
(3)如图③,在锐角△ABC中,BD和BE三等分外角∠PBC,CD和CE三等分外角∠QCB,请分别直接写出∠A和∠D,∠A和∠E的数量关系.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,抛物线y=ax2+![]() x+c过A(﹣1,0),B(0,2)两点.
x+c过A(﹣1,0),B(0,2)两点.
(1)求抛物线的解析式.
(2)M为抛物线对称轴与x轴的交点,N为x轴上对称轴上任意一点,若tan∠ANM=![]() ,求M到AN的距离.
,求M到AN的距离.
(3)在抛物线的对称轴上是否存在点P,使△PAB为等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】周末,小明和哥哥一起骑自行车从家里出发到昌南湖游玩,从家出发0.5小时后到达陶溪川,游玩一段时间后按原速前往昌南湖.小明离家80分钟后,爸爸驾车沿相同路线前往昌南湖,如图是他们离家的路程y(km)与小明离家时间x(h)的函数图象,已知爸爸驾车的速度是小明骑车速度的3倍.
(1)小明骑车的速度为_____km/h,爸爸驾车的速度为_____km/h.
(2)小明从家到陶溪川的路程y与时间x的函数关系式为_____,他从陶溪川到昌南湖的路程y与时间x的函数关系式为______,爸爸从家到昌南湖的路程,与时间x的函数关系式为______.
(3)小明从家出发多少小时后被爸爸追上?此时离家多远?
(4)如果小明比爸爸晚10分钟到达昌南湖,那么昌南湖离家有多远?

查看答案和解析>>
科目: 来源: 题型:
【题目】某市在党中央实施“精准扶贫”政策的号召下,大力开展科技扶贫工作,帮助农民组建农副产品销售公司,某农副产品的年产量不超过100万件,该产品的生产费用y(万元)与年产量x(万件)之间的函数图象是顶点为原点的抛物线的一部分(如图①所示);该产品的销售单价z(元/件)与年销售量x(万件)之间的函数图象是如图②所示的一条线段,生产出的产品都能在当年销售完,达到产销平衡,所获毛利润为w万元.(毛利润=销售额﹣生产费用)

(1)请直接写出y与x以及z与x之间的函数关系式;
(2)求w与x之间的函数关系式;并求年产量多少万件时,所获毛利润最大?最大毛利润是多少?
(3)由于受资金的影响,今年投入生产的费用不会超过360万元,今年最多可获得多少万元的毛利润?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com