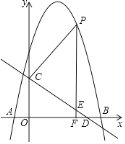
【题目】如图，抛物线与轴交于、两点，直线与轴交于点，与轴交于点．点是抛物线上一动点，过点作直线轴于点，交直线于点．设点的横坐标为．

求抛物线的解析式；

若点在轴上方的抛物线上，当时，求点的坐标；

若点’是点关于直线的对称点，当点’落在轴上时，请直接写出的值．

（1）求证：△BDC≌△EFC；

（2）若EF∥CD，求证：∠BDC＝90°．

将一张如图①所示的“完美筝形”纸片ABCD先折叠成如图②所示形状,再展开得到图③,其中CE,CF为折痕,∠BCE=∠ECF=∠FCD,点B′为点B的对应点,点D′为点D的对应点,连接EB',FD′相交于点O．

简单应用：

(1)在平行四边形、矩形、菱形、正方形四种图形中,一定为“完美筝形”的是__________________．

(2)请你结合图1写出一条完美筝形的性质_______________．

(3)当图3中的∠BCD=120°时,∠AEB′=_________________．

(4)当图2中的四边形AECF为菱形时,对应图③中的“完美筝形”有__________________________(写出筝形的名称：例 筝形ABCD)．

【题目】要建一个如图所示的面积为300 的长方形围栏，围栏总长50m，一边靠墙（墙长25m），

（1）求围栏的长和宽；

（2）能否围成面积为400 的长方形围栏？如果能，求出该长方形的长和宽，如果不能请说明理由。

【题目】已知二次函数的部分图象如图所示，则关于的一元二次方程的解为 ．

证明：

【题目】已知二次函数的图象如图所示，则下列结论：①；②；③；④，其中正确的结论的序号是（ ）

A. ①② B. ①③ C. ③④ D. ②④

【题目】已知：线段AB，BC，．

求作：矩形ABCD．

老师说甲、乙同学的作图都正确. 请你选择其中一位同学的作业说明其作图依据.

我选择____同学，他的作图依据是：___________________________________________.

(1)如图1，当点P在线段AO上时，试猜想PE与PD的数量关系和位置关系，不用说明理由；

(2)如图2，当点P在线段OC上时，(1)中的猜想还成立吗？请说明理由；

(3)如图3，当点P在AC的延长线上时，请你在图3中画出相应的图形(尺规作图，保留作图痕迹，不写作法)，并判断(1)中的猜想是否成立？若成立，请直接写出结论；若不成立，请说明理由．