
科目: 来源: 题型:
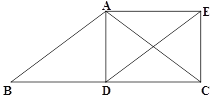
【题目】如图,在△ABC中,AB = AC,点D是边BC的中点,过点A、D分别作BC与AB的平行线,相交于点E,连结EC、AD.
求证:四边形ADCE是矩形.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,△ABC中,∠ABC与∠ACB的平分线交于点F,过点F作DE∥BC交AB于点D,交AC于点E,那么下列结论,①△BDF是等腰三角形;②DE=BD+CE;③若∠A=50°,∠BFC=105°;④BF=CF.其中正确的有( )
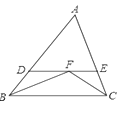
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目: 来源: 题型:
【题目】(2017怀化,第10题,4分)如图,A,B两点在反比例函数![]() 的图象上,C,D两点在反比例函数
的图象上,C,D两点在反比例函数![]() 的图象上,AC⊥y轴于点E,BD⊥y轴于点F,AC=2,BD=1,EF=3,则
的图象上,AC⊥y轴于点E,BD⊥y轴于点F,AC=2,BD=1,EF=3,则![]() 的值是( )
的值是( )

A. 6 B. 4 C. 3 D. 2
查看答案和解析>>
科目: 来源: 题型:
【题目】晓东在解一元二次方程时,发现有这样一种解法:如:解方程x(x+4)=6.
解:原方程可变形,得[(x+2)﹣2][(x+2)+2]=6.(x+2)2﹣22=6,(x+2)2=6+22,(x+2)2=10.直接开平方并整理,得![]() ,
,![]() .我们称晓东这种解法为“平均数法”.
.我们称晓东这种解法为“平均数法”.
(1)下面是晓东用“平均数法”解方程(x+2)(x+6)=5时写的解题过程.
解:原方程可变形,得
[(x+□)﹣〇][(x+□)+〇]=5.
(x+□)2﹣〇2=5,
(x+□)2=5+〇2.
直接开平方并整理,得x1=☆,x2=¤.
上述过程中的“□”,“〇”,“☆”,“¤”表示的数分别为 , , , .
(2)请用“平均数法”解方程:(x﹣3)(x+1)=5.
查看答案和解析>>
科目: 来源: 题型:
【题目】某中学课外活动小组准备围建一个矩形生物苗圃园,其中一边靠墙,另外三边用长为![]() 米的篱笆围成,已知墙长为
米的篱笆围成,已知墙长为![]() 米.设这个苗圃园垂直于墙的一边的长为
米.设这个苗圃园垂直于墙的一边的长为![]() 米某中学课外活动小组准备围建一个矩形生物苗圃园,其中一边靠墙,另外三边用长为
米某中学课外活动小组准备围建一个矩形生物苗圃园,其中一边靠墙,另外三边用长为![]() 米的篱笆围成,已知墙长为
米的篱笆围成,已知墙长为![]() 米.设这个苗圃园垂直于墙的一边的长为
米.设这个苗圃园垂直于墙的一边的长为![]() 米
米
![]() 用含
用含![]() 的代数式表示平行于墙的一边的长为________米,
的代数式表示平行于墙的一边的长为________米,![]() 的取值范围为________;
的取值范围为________;
![]() 这个苗圃园的面积为
这个苗圃园的面积为![]() 平方米时,求
平方米时,求![]() 的值.
的值.

查看答案和解析>>
科目: 来源: 题型:
【题目】某数学兴趣小组对关于![]() 的方程
的方程![]() 提出了下列问题.
提出了下列问题.
![]() 若使方程为一元二次方程,
若使方程为一元二次方程,![]() 是否存在?若存在,求出
是否存在?若存在,求出![]() 并解此方程.
并解此方程.
![]() 若使方程为一元一次方程,
若使方程为一元一次方程,![]() 是否存在?若存在,请求出.你能解决这个问题吗?
是否存在?若存在,请求出.你能解决这个问题吗?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,点![]() 分别是
分别是![]() 轴上位于原点两侧的两点,点
轴上位于原点两侧的两点,点![]() 在第一象限,直线
在第一象限,直线![]() 交
交![]() 轴于点
轴于点![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() ,
,![]() .
.
(1)求![]() ;
;
(2)求点![]() 的坐标及
的坐标及![]() 的值;
的值;
(3)若![]() ,求直线
,求直线![]() 的函数表达式.
的函数表达式.

查看答案和解析>>
科目: 来源: 题型:
【题目】在国家的宏观调控下,某市的商品房成交价由今年3月份的5000元/m2下降到5月份的4050元/m2.
(1)问4、5两月平均每月降价的百分率是多少?
(2)如果房价继续回落,按此降价的百分率,你预测到7月分该市的商品房成交均价是否会跌破3000元/m2?请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读下列一段文字,然后回答下列问题.
已知在平面内有两点P1 x1,y1 ,P1 x2,y2 其两点间的距离P1P2 = ![]() ,同时,当两点所在的直线在坐标轴或平行于坐标轴或垂直于坐标轴时,两点间距离公式可化简为|x2 x1|或|y2 y1|.
,同时,当两点所在的直线在坐标轴或平行于坐标轴或垂直于坐标轴时,两点间距离公式可化简为|x2 x1|或|y2 y1|.
(1)已知 A (1,4)、B (-3,5),试求 A.、B两点间的距离;
(2)已知 A、B在平行于 y轴的直线上,点 A的纵坐标为-8,点 B的纵坐标为-1,试求 A、B两点的距 离;
(3)已知一个三角形各顶点坐标为 D(1,6)、E(-2,2)、F(4,2),你能判定此三角形的形状吗?说明理由:
(4)在(3)的条件下,平面直角坐标系中,在 x轴上找一点 P,使 PD+PF的长度最短,求出点 P的坐 标以及 PD+PF的最短长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com