
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 是第一、三象限的角平分线.
是第一、三象限的角平分线.

(1)由图观察易知A(0,2)关于直线l的对称点A′的坐标为(2,0),请在图中分别标明B(5,3)、C(-2,5)关于直线l的对称点B′、C′的位置,并写出他们的坐标:![]() ___________、
___________、![]() ___________;
___________;
(2)结合图形观察以上三组点的坐标,你会发现:坐标平面内任一点![]() 关于第一、三象限的角平分线
关于第一、三象限的角平分线![]() 的对称点
的对称点![]() 的坐标为___________(不必证明);
的坐标为___________(不必证明);
(3)已知两点![]() 、
、![]() ,试在直线L上画出点Q,使点Q到D、E两点的距离之和最小,求QD+QE的最小值.
,试在直线L上画出点Q,使点Q到D、E两点的距离之和最小,求QD+QE的最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知,如图,△ABC和△ECD都是等腰直角三角形,∠ACD=∠DCE=90°,D为AB边上一点.求证:(1)BD=AE.(2)若线段AD=5,AB=17,求线段ED的长。

查看答案和解析>>
科目: 来源: 题型:
【题目】农夫将苹果树种在正方形的果园内,为了保护苹果树不受风吹,他在苹果树的周围种上针叶树.在下图里,你可以看到农夫所种植苹果树的列数(n)和苹果树数量及针叶树数量的规律:当n为某一个数值时,苹果树数量会等于针叶树数量,则n为___________

查看答案和解析>>
科目: 来源: 题型:
【题目】放置在水平桌面上的台灯的灯臂AB长为40 cm,灯罩BC长为30 cm,底座厚度为2 cm,灯臂与底座构成的∠BAD=60°.使用发现,光线最佳时灯罩BC与水平线所成的角为30°,此时灯罩顶端C到桌面的高度CE是多少厘米?(结果精确到0.1 cm,参考数据:![]() ≈1.732)
≈1.732)


查看答案和解析>>
科目: 来源: 题型:
【题目】某城市出租汽车收费标准为:![]() 以内(含
以内(含![]() )收费
)收费![]() 元;超出
元;超出![]() 的部分,每千米收费
的部分,每千米收费![]() 元.
元.
(1)写出车费![]() 元与行驶路程x(km)之间的函数关系式(
元与行驶路程x(km)之间的函数关系式(![]() ≥4);
≥4);
(2)某人乘出租汽车行驶了5 km,应付多少车费;
(3)若某人付了![]() 元车费,那么出租车行驶了多远.
元车费,那么出租车行驶了多远.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点 B、O分别落在点 B1、C1 处,点B1在x轴上,再将△AB1C1 绕点 B1 顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2 绕点C2 顺时针旋转到△A2B2C2 的位置,点 A2 在x轴上,依次进行下去….若点 A(![]() ,0),B(0,4),则点 B2016 的横坐标为_______.
,0),B(0,4),则点 B2016 的横坐标为_______.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知AD与BC相交于点O,AC⊥BC于点C,BD⊥AD于点D,添加下列条件中的一个条件:其中能够使△ABC≌△BAD的条件的个数有( )
(1)AC=BD ;(2)OC=OD ;(3)∠CAO=∠D B O ;(4)∠CAB=∠D B A
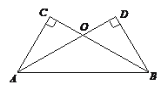
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目: 来源: 题型:
【题目】将平行四边形纸片ABCD按如图方式折叠,使点C与A重合,点D落到D′处,折痕为EF.

(1)求证:△ABE≌△AD′F;
(2)连接CF,判断四边形AECF是什么特殊四边形?证明你的结论.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知,如图,一次函数y=kx+b(k、b为常数,k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数y=![]() (n为常数且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂直为D,若OB=2OA=3OD=6.
(n为常数且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂直为D,若OB=2OA=3OD=6.
(1)求一次函数与反比例函数的解析式;
(2)求两函数图象的另一个交点坐标;
(3)直接写出不等式;kx+b≤![]() 的解集.
的解集.

查看答案和解析>>
科目: 来源: 题型:
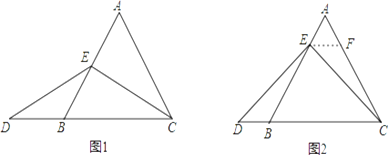
【题目】已知,在等边三角形ABC中,点E在AB上,点D在CB的延长线上,且ED=EC.
(1)(特殊情况,探索结论)
如图1,当点E为AB的中点时,确定线段AE与DB的大小关系,请你直接写出结论:
AE DB(填“>”、“<”或“=”).
(2)(特例启发,解答题目)
如图2,当点E为AB边上任意一点时,确定线段AE与DB的大小关系,请你直接写出结论,AE DB(填“>”、“<”或“=”);理由如下,过点E作EF∥BC,交AC于点F.(请你将解答过程完整写下来).
(3)(拓展结论,设计新题)
在等边三角形ABC中,点E在直线AB上,点D在线段CB的延长线上,且ED=EC,若△ABC的边长为1,AE=2,求CD的长.(请你画出相应图形,并直接写出结果).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com