
科目: 来源: 题型:
【题目】某药厂销售部门根据市场调研结果,对该厂生产的一种新型原料药未来两年的销售进行预测,井建立如下模型:设第t个月该原料药的月销售量为P(单位:吨),P与t之间存在如图所示的函数关系,其图象是函数P=![]() (0<t≤8)的图象与线段AB的组合;设第t个月销售该原料药每吨的毛利润为Q(单位:万元),Q与t之间满足如下关系:Q=
(0<t≤8)的图象与线段AB的组合;设第t个月销售该原料药每吨的毛利润为Q(单位:万元),Q与t之间满足如下关系:Q=![]()
(1)当8<t≤24时,求P关于t的函数解析式;
(2)设第t个月销售该原料药的月毛利润为w(单位:万元)
①求w关于t的函数解析式;
②该药厂销售部门分析认为,336≤w≤513是最有利于该原料药可持续生产和销售的月毛利润范围,求此范围所对应的月销售量P的最小值和最大值.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,点P是![]() 的角平分线OC上一点,PN
的角平分线OC上一点,PN![]() OB于点N,点M是线段ON上一点,已知OM=3,ON=4,点D为OA上一点,若满足PD=PM,则OD的长度为________
OB于点N,点M是线段ON上一点,已知OM=3,ON=4,点D为OA上一点,若满足PD=PM,则OD的长度为________

查看答案和解析>>
科目: 来源: 题型:
【题目】“绿水青山就是金山银山”的理念已融入人们的日常生活中,因此,越来越多的人喜欢骑自行车出行.某自行车店在销售某型号自行车时,以高出进价的50%标价.已知按标价九折销售该型号自行车8辆与将标价直降100元销售7辆获利相同.
(1)求该型号自行车的进价和标价分别是多少元?
(2)若该型号自行车的进价不变,按(1)中的标价出售,该店平均每月可售出51辆;若每辆自行车每降价20元,每月可多售出3辆,求该型号自行车降价多少元时,每月获利最大?最大利润是多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】小明在一次打篮球时,篮球传出后的运动路线为如图所示的抛物线,以小明所站立的位置为原点O建立平面直角坐标系,篮球出手时在O点正上方1m处的点P.已知篮球运动时的高度y(m)与水平距离x(m)之间满足函数表达式y=-![]() x2+x+c.
x2+x+c.
(1)求y与x之间的函数表达式;
(2)球在运动的过程中离地面的最大高度;
(3)小亮手举过头顶,跳起后的最大高度为BC=2.5m,若小亮要在篮球下落过程中接到球,求小亮离小明的最短距离OB.

查看答案和解析>>
科目: 来源: 题型:
【题目】两幢大楼的部分截面及相关数据如图,小明在甲楼A处透过窗户E发现乙楼F处出现火灾,此时A,E,F在同一直线上.跑到一楼时,消防员正在进行喷水灭火,水流路线呈抛物线,在1.2m高的D处喷出,水流正好经过E,F. 若点B和点E、点C和F的离地高度分别相同,现消防员将水流抛物线向上平移0.4m,再向左后退了____m,恰好把水喷到F处进行灭火.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,等腰△ABC的底边BC的长为2cm,面积是6cm2,腰AB的垂直平分线EF交AB于点E,交AC于点F.若D为BC边上的中点,M为线段EF上一动点,则△BDM的周长最短为____________cm.
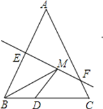
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,△ABC是等边三角形,△ABD是等腰直角三角形,∠BAD=90°,AE⊥BD与点E,连CD分别交AE、AB于点F、G,过点A作AH⊥CD交BD于点H,则下列结论:①∠ADC=15°;②AF=AG;③△ADF≌△BAH;④ DF=2EH,其中正确结论的个数为( )
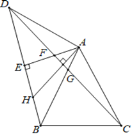
A.4B.3C.2D.1
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,Rt△ABC中,∠C=90°,以点B为圆心,适当长为半径画弧,与∠ABC的两边相交于点E,F,分别以点E和点F为圆心,大于![]() EF的长为半径画弧,两弧相交于点M,作射线BM,交AC于点D.若△BDC的面积为10,∠ABC=2∠A,则△ABC的面积为( )
EF的长为半径画弧,两弧相交于点M,作射线BM,交AC于点D.若△BDC的面积为10,∠ABC=2∠A,则△ABC的面积为( )
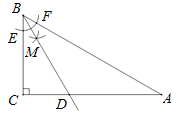
A.25B.30C.35D.40
查看答案和解析>>
科目: 来源: 题型:
【题目】某公司销售某一种新型通讯产品,已知每件产品的进价为4万元,每月销售该种产品的总开支(不含进价)总计11万元.在销售过程中发现,月销售量夕(件)与销售单价x (万元)之间存在着如图所示的一次函数关系、
(1)求y关于x的函数关系式(直接写出结果)
(2)试写出该公司销售该种产品的月获利z(万元)关于销售单价x(万元)的函数关系式、当销售单价x为何值时,月获利最大?并求这个最大值(月获利一月销售额一月销售产品总进价一月总开支)
(3)若公司希望该产品一个月的销售获利不低于5万元,借助(2)中函数的图象,请你帮助该公司确定销售单价的范围.在此情况下,要使产品销售量最大,你认为销售单价应定为多少万元

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com