
科目: 来源: 题型:
【题目】如图,设一个三角形的三边分别是3,13m,8.

(1)求m的取值范围;
(2)是否存在整数m使三角形的周长为偶数?若存在,求出三角形的周长;若不存在,说明理由;
(3)如图,在(2)的条件下,当AB=8,AC=13m,BC=3时,若D是AB的中点,连CD,P是CD上动点(不与C,D重合,当P在线段CD上运动时,有两个式子):①![]() ;②
;②![]() ,其中有一个的值不变,另一个的值改变。问题:
,其中有一个的值不变,另一个的值改变。问题:
A.请判断出谁不变,谁改变;
B.若不变的求出其值,若改变的求出变化的范围。
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系中,二次函数y=x2+bx+c(b,c都是常数)的图象经过点(1,0)和(0,2).
(1)当﹣2≤x≤2时,求y的取值范围.
(2)已知点P(m,n)在该函数的图象上,且m+n=1,求点P的坐标.
查看答案和解析>>
科目: 来源: 题型:
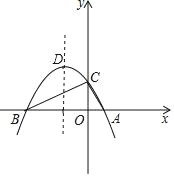
【题目】如图,抛物线y=﹣![]() x2+bx+2与x轴交于A,B两点,与y轴交于C点,且点A的坐标为(1,0).
x2+bx+2与x轴交于A,B两点,与y轴交于C点,且点A的坐标为(1,0).
(1)求抛物线的解析式及顶点D的坐标;
(2)判断△ABC的形状,并证明你的结论;
(3)点M是抛物线对称轴上的一个动点,当△ACM的周长最小时,求点M的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】某校七年级准备购买一批笔记本奖励优秀学生,在购买时发现,每本笔记本可以打九折,用360元钱购买的笔记本,打折后购买的数量比打折前多10本.
(1)求打折前每本笔记本的售价是多少元?
(2)由于考虑学生的需求不同,学校决定购买笔记本和笔袋共90件,笔袋每个原售价为6元,两种物品都打九折,若购买总金额不低于360元,且不超过365元,问有哪几种购买方案?
查看答案和解析>>
科目: 来源: 题型:
【题目】已知二次函数y=﹣x2+4x.
(1)写出二次函数y=﹣x2+4x图象的对称轴;
(2)在给定的平面直角坐标系中,画出这个函数的图象(列表、描点、连线);
(3)根据图象,写出当y<0时,x的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,AD为△ABC的中线,BE为△ABD的中线.
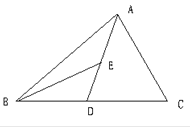
(1)∠ABE=15°,∠BAD=40°,求∠BED的度数;
(2)在△BED中作BD边上的高;
(3)若△ABC的面积为40,BD=5,则△BDE 中BD边上的高为多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,抛物线![]() 与x轴交于点A,B,与
与x轴交于点A,B,与![]() 轴交于点C。过点C作CD∥x轴,交抛物线的对称轴于点D,连结BD。已知点A坐标为(-1,0)。
轴交于点C。过点C作CD∥x轴,交抛物线的对称轴于点D,连结BD。已知点A坐标为(-1,0)。

(1)求该抛物线的解析式;
(2)求梯形COBD的面积。
查看答案和解析>>
科目: 来源: 题型:
【题目】两组邻边分别相等的四边形叫做“筝形”,如图,四边形ABCD是一个筝形,其中![]() ,
,![]() ,詹姆斯在探究筝形的性质时,得到如下结论:
,詹姆斯在探究筝形的性质时,得到如下结论:![]() ;
;![]() ;
;![]() ≌
≌![]() ;
;![]() 四边形ABCD的面积
四边形ABCD的面积![]() 其中正确的结论有
其中正确的结论有![]()
![]()

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目: 来源: 题型:
【题目】若二次函数y=﹣x2+4x+c的图象经过A(1,y1),B(﹣1,y2),C(2+ ![]() ,y3)三点,则y1、y2、y3的大小关系是( )
,y3)三点,则y1、y2、y3的大小关系是( )
A. y1<y2<y3 B. y1<y3<y2 C. y2<y3<y1 D. y2<y1<y3
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c的图象与x轴交于点A(﹣1,0),与y轴的交点B在(0,2)与(0,3)之间(不包括这两点),对称轴为直线x=2.下列结论:abc<0;②9a+3b+c>0;③若点M(![]() ,y1),点N(
,y1),点N(![]() ,y2)是函数图象上的两点,则y1<y2;④﹣
,y2)是函数图象上的两点,则y1<y2;④﹣![]() <a<﹣
<a<﹣![]() .其中正确结论有( )
.其中正确结论有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com