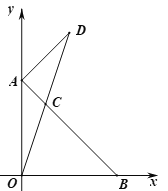
【题目】在平面直角坐标系中，点A(0,m)和点B(n,0)分别在y轴和x轴的正半轴上，满足，连接线段AB，点C为AB上一动点.

(1)填空:m=_____，n=_____；

(2)如图，连接OC并延长至点D，使得DC=OC，连接AD.若△AOC的面积为2，求点D的坐标；

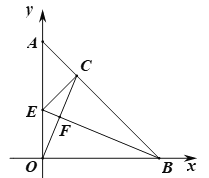
(3)如图，BC=OB，∠ABO的平分线交线段AO于点E，交线段OC于点F，连接EC.

求证：①△ACE为等腰直角三角形;

②BF－EF=OC.

【题目】如图，抛物线y=﹣x2+bx+c与x轴交于点A（﹣1，0）和点B，与y轴交于C（0，3），直线y=+m经过点C，与抛物线的另一交点为点D，点P是直线CD上方抛物线上的一个动点，过点P作PF⊥x轴于点F，交直线CD于点E，设点P的横坐标为m．

（1）求抛物线解析式并求出点D的坐标；

（2）连接PD，△CDP的面积是否存在最大值？若存在，请求出面积的最大值；若不存在，请说明理由；

（3）当△CPE是等腰三角形时，请直接写出m的值．

(1)①如图，若∠BAC=36o，求证：BD=EF；

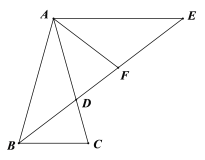
②如图，若∠BAC=60o，求的值；

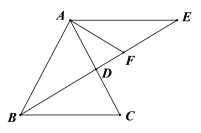
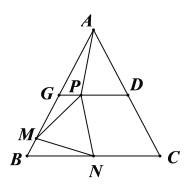
(2)如图，若∠BAC=60o，过点D作DG// BC，交AB于点G，点N为BC中点，点P, M分别是GD, BG上的动点，且∠PNM=60°. 求证：AP=PN=MN.

（2）拓展探究：如图2，当△ABC绕点A逆时针旋转θ（0°＜θ＜90°）时，BD=CF成立吗？若成立，请证明；若不成立，请说明理由．

（3）解决问题：如图3，当△ABC绕点A逆时针旋转45°时，延长BD交CF于点H．

①求证：BD⊥CF；

②当AB=2，AD=3时，则线段DH的长为　 　．

（1）求这15辆车中大小货车各多少辆？

（2）现安排其中10辆货车前往A村，其余货车前往B村，设前往A村的大货车为x辆，前往A、B两村总费用为y元，试求出y与x的函数解析式．

（3）在（2）的条件下，若运往A村的鱼苗不少于100箱，请你写出使总费用最少的货车调配方案，并求出最少费用．

【题目】如图，在直角坐标系中，Rt△ABC的直角边AC在x轴上，∠ACB=90°，AC=1，反比例函数y=（k＞0）的图象经过BC边的中点D（3，1）．

（1）求这个反比例函数的表达式；

（2）若△ABC与△EFG成中心对称，且△EFG的边FG在y轴的正半轴上，点E在这个函数的图象上．

①求OF的长；

②连接AF，BE，证明四边形ABEF是正方形．

【题目】如图，山顶建有一座铁塔，塔高BC=80米，测量人员在一个小山坡的P处测得塔的底部B点的仰角为45°，塔顶C点的仰角为60°．已测得小山坡的坡角为30°，坡长MP=40米．求山的高度AB（精确到1米）．（参考数据：≈1.414，≈1.732）

（1）求证：AE=AD．

（2）若AE=3，CD=4，求AB的长．

(1)请用含a和x的代数式分别表示在武汉以及上海购进的羽绒服的单价(单位:元/件);

(2)若服装店老板两次进货共花费17.84万元，在销售这款羽绒服时每件定价都是 1200元，第二次销售后期由于天气转暖，服装还剩没有卖出，老板决定打8折销售，最后全部售完.两次销售，服装店老板共盈利多少元?

调查结果统计表

根据以上信息解答下列问题：

（1）统计表中，a=　 　，b=　 　，c=　 　；

（2）扇形统计图中，m的值为　 　，“C”所对应的圆心角的度数是　 　；

（3）若参加本次竞赛的同学共有5000人，请你估计成绩在95分及以上的学生大约有多少人？