
科目: 来源: 题型:
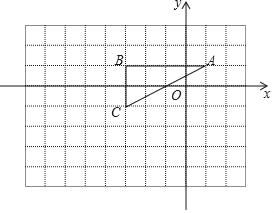
【题目】如图所示,在平面直角坐标系中有一格点三角形,该三角形的三个顶点为:A(1,1),B(﹣3,1),C(﹣3,﹣1).
(1)若△ABC的外接圆的圆心为P,则点P的坐标为_____,⊙P的半径为_____;
(2)如图所示,在11×8的网格图内,以坐标原点O点为位似中心,将△ABC按相似比2:1放大,A、B、C的对应点分别为A'、B'、C'.①画出△A'B'C';②将△A'B'C'沿x轴方向平移,需平移_____个单位长度,能使得B'C'所在的直线与⊙P相切.
查看答案和解析>>
科目: 来源: 题型:
【题目】我们知道,假分数可以化为整数与真分数的和的形式,例如:![]() .
.
在分式中,对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时,我们称之为“假分式”;当分子的次数小于分母的次数时,我们称之为“真分式”.
例如:像![]() ,
,![]() ,…这样的分式是假分式;像
,…这样的分式是假分式;像![]() ,
,![]() ,…这样的分式是真分式.
,…这样的分式是真分式.
类似的,假分式也可以化为整式与真分式的和(差)的形式.
例如:将分式![]() 拆分成一个整式与一个真分式的和(差)的形式.
拆分成一个整式与一个真分式的和(差)的形式.
方法一:解:由分母为![]() ,可设
,可设![]()
则由![]()
对于任意![]() ,上述等式均成立,
,上述等式均成立,
∴![]() ,解得
,解得![]()
∴![]()
这样,分式![]() 就被拆分成一个整式与一个真分式的和(差)的形式.
就被拆分成一个整式与一个真分式的和(差)的形式.
方法二:解:
![]()
这样,分式![]() 就拆分成一个整式与一个真分式的和(差)的形式.
就拆分成一个整式与一个真分式的和(差)的形式.
(1)请仿照上面的方法,选择其中一种方法将分式![]() 拆分成一个整式与一个真分式的和(差)的形式;
拆分成一个整式与一个真分式的和(差)的形式;
(2)已知整数![]() 使分式
使分式![]() 的值为整数,求出满足条件的所有整数
的值为整数,求出满足条件的所有整数![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知二次函数y=x2﹣4x+3.
(1)用配方法将此二次函数化为顶点式;
(2)求出它的顶点坐标和对称轴;
(3)求出二次函数的图象与x轴的两个交点坐标;
(4)在所给的坐标系上,画出这个二次函数的图象;
(5)观察图象填空,使y随x的增大而减小的x的取值范围是_____.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,点P是菱形ABCD边上的一动点,它从点A出发沿在A→B→C→D路径匀速运动到点D,设△PAD的面积为y,P点的运动时间为x,则y关于x的函数图象大致为( )

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目: 来源: 题型:
【题目】为了“迎国庆,向祖国母亲献礼”,某建筑公司承建了修筑一段公路的任务,指派甲、乙两队合作,18天可以完成,共需施工费126000元;如果甲、乙两队单独完成此项工程,乙队所用时间是甲队的1.5倍,乙队每天的施工费比甲队每天的施工费少1000元.
(1)甲、乙两队单独完成此项工程,各需多少天?
(2)为了尽快完成这项工程任务,甲、乙两队通过技术革新提高了速度,同时,甲队每天的施工费提高了![]() ,乙队每天的施工费提高了
,乙队每天的施工费提高了![]() ,已知两队合作12天后,由甲队再单独做2天就完成了这项工程任务,且所需施工费比计划少了21200元.
,已知两队合作12天后,由甲队再单独做2天就完成了这项工程任务,且所需施工费比计划少了21200元.
①分别求出甲、乙两队技术革新前每天的施工费用;
②求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,以
,以![]() 为直径的
为直径的![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() ,在
,在![]() 上取一点
上取一点![]() ,使
,使![]() ,连接
,连接![]() ,对于下列结论:①
,对于下列结论:①![]() ;②
;②![]() ;③弧
;③弧![]() 弧
弧![]() ;④
;④![]() 为
为![]() 的切线,结论一定正确的是( )
的切线,结论一定正确的是( )

A. ②③ B. ②④ C. ①② D. ①③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com