
科目: 来源: 题型:
【题目】如图,直线y=x+3与坐标轴分别交于A,B两点,抛物线y=ax2+bx-3a经过点A,B,顶点为C,连接CB并延长交x轴于点E,点D与点B关于抛物线的对称轴MN对称.

(1)求抛物线的解析式及顶点C的坐标;
(2)求证:四边形ABCD是直角梯形.
【答案】(1)y=-x2-2x+3,顶点C的坐标为(-1,4);(2)证明见解析.
【解析】
(1)解:∵y=x+3与坐标轴分别交与A,B两点,∴A点坐标(-3,0)、B点坐标(0,3).
∵抛物线y=ax2+bx-3a经过A,B两点,
∴![]()
解得![]()
∴抛物线解析式为:y=-x2-2x+3.
∵y=-x2-2x+3=-(x+1)2+4,
∴顶点C的坐标为(-1,4).
(2)证明:∵B,D关于MN对称,C(-1,4),B(0,3),
∴D(-2,3).∵B(0,3),A(-3,0),∴OA=OB.
又∠AOB=90°,∴∠ABO=∠BAO=45°.
∵B,D关于MN对称,∴BD⊥MN.
又∵MN⊥x轴,∴BD∥x轴.
∴∠DBA=∠BAO=45°.
∴∠DBO=∠DBA+∠ABO=45°+45°=90°.
设直线BC的解析式为y=kx+b,
把B(0,3),C(-1,4)代入得,
![]() 解得
解得![]()
∴y=-x+3.
当y=0时,-x+3=0,x=3,∴E(3,0).
∴OB=OE,又∵∠BOE=90°,
∴∠OEB=∠OBE=∠BAO=45°.
∴∠ABE=180°-∠BAE-∠BEA=90°.
∴∠ABC=180°-∠ABE=90°.
∴∠CBD=∠ABC-∠ABD=45°.
∵CM⊥BD,∴∠MCB=45°.
∵B,D关于MN对称,
∴∠CDM=∠CBD=45°,CD∥AB.
又∵AD与BC不平行,∴四边形ABCD是梯形.
∵∠ABC=90°,∴四边形ABCD是直角梯形.
【题型】解答题
【结束】
21
【题目】有两组卡片,第一组三张卡片上都写着A、B、B,第二组五张卡片上都写着A、B、B、D、E.试用列表法求出从每组卡片中各抽取一张,两张都是B的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,AF平分∠CAB,交CD于点E,交CB于点F.若AC=6,AB=10,则DE的长为______

查看答案和解析>>
科目: 来源: 题型:
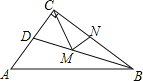
【题目】如图,△ABC中,∠ACB=90°,AC =3,BC =4,AB=5,BD平分∠ABC,如果M、N分别为BD、BC上的动点,那么CM+MN的最小值是____.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,某水平地面上建筑物的高度为AB,在点D和点F处分别竖立高是2米的标杆CD和EF,两标杆相隔52米,并且建筑物AB,标杆CD和EF在同一竖直平面内,从标杆CD后退2米到点G处,在G处测得建筑物顶端A和标杆顶端C在同一条直线上;从标杆FE后退4米到点H处,在H处测得建筑物顶端A和标杆顶端E在同一条直线上,求建筑物的高.

查看答案和解析>>
科目: 来源: 题型:
【题目】已知a:b:c=2:3:4,且2a+3b﹣2c=10,求a﹣2b+3c的值.
【答案】16.
【解析】试题根据比例的性质可设a=2k,b=3k,c=4k,则利用2a+3b-2c=10得到4k+9k-8k=10,解得k=2,于是可求出a、b、c的值,然后计算a-2b+3c的值.
试题解析:∵a:b:c=2:3:4,
∴设a=2k,b=3k,c=4k,
而2a+3b-2c=10,
∴4k+9k-8k=10,解得k=2,
∴a=4,b=6,c=8,
∴a-2b+3c=4-12+24=16.
考点:比例的性质.
【题型】解答题
【结束】
24
【题目】计算:![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】(4分)一元二次方程![]() 的根的情况是( )
的根的情况是( )
A.有两个不相等的实数根 B.有两个相等的实数根
C.没有实数根 D.无法确定
【答案】A.
【解析】
试题∵△=![]() ,∴方程有两个不相等的实数根.故选A.
,∴方程有两个不相等的实数根.故选A.
考点:根的判别式.
【题型】单选题
【结束】
9
【题目】已知直线y=kx(k>0)与双曲线![]() 交于点A(x1,y1),B(x2,y2)两点,则x1y2+x2y1的值为【 】
交于点A(x1,y1),B(x2,y2)两点,则x1y2+x2y1的值为【 】
A.﹣6 B.﹣9 C.0 D.9
查看答案和解析>>
科目: 来源: 题型:
【题目】已知直线y=kx(k>0)与双曲线![]() 交于点A(x1,y1),B(x2,y2)两点,则x1y2+x2y1的值为【 】
交于点A(x1,y1),B(x2,y2)两点,则x1y2+x2y1的值为【 】
A.﹣6 B.﹣9 C.0 D.9
【答案】A。
【解析】∵点A(x1,y1),B(x2,y2)是双曲线![]() 上的点,∴x1y1=x2y2=3。
上的点,∴x1y1=x2y2=3。
∵直线y=kx(k>0)与双曲线![]() 交于点A(x1,y1),B(x2,y2)两点,∴x1=﹣x2,y1=﹣y2
交于点A(x1,y1),B(x2,y2)两点,∴x1=﹣x2,y1=﹣y2
∴x1y2+x2y1=﹣x1y1﹣x2y2=﹣3﹣3=﹣6。故选A。
【题型】单选题
【结束】
10
【题目】在一个不透明的口袋中,装有红色、黑色、白色的玻璃球共40个,除颜色外其余都相同,小明通过许多次摸球实验后发现,其中摸到红色球、黑色球的频率稳定在15%和45%,则口袋中白色球的个数可能是( )
A. 18 B. 17 C. 16 D. 15
查看答案和解析>>
科目: 来源: 题型:
【题目】为倡导低碳生活,绿色出行,某自行车俱乐部利用周末组织“远游骑行”活动,自行车队从甲地出发,目的地为乙地,在自行车队出发![]() 小时后,恰有一辆邮政车从甲地出发,沿自行车队行进路线前往乙地,到达乙地后立即按原路返回甲地.自行车队与邮政车行驶速度均保持不变,并且邮政车行驶速度是自行车队行驶速度的
小时后,恰有一辆邮政车从甲地出发,沿自行车队行进路线前往乙地,到达乙地后立即按原路返回甲地.自行车队与邮政车行驶速度均保持不变,并且邮政车行驶速度是自行车队行驶速度的![]() 倍.如图所示的是自行车队、邮政车离甲地的路程
倍.如图所示的是自行车队、邮政车离甲地的路程![]() 与自行车队离开甲地的时间
与自行车队离开甲地的时间![]() 的关系图象,请根据图象提供的信息,回答下列问题.
的关系图象,请根据图象提供的信息,回答下列问题.

(1)自行车队行驶的速度是 ;邮政车行驶的速度是 ;![]() .
.
(2)邮政车出发多少小时与自行车队相遇?
(3)当邮政车与自行车队相距![]() 时,此时离邮政车出发经过了多少小时?
时,此时离邮政车出发经过了多少小时?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com