
科目: 来源: 题型:
【题目】我市某中学决定在学生中开展丢沙包、打篮球、跳大绳和踢毽球四种项目的活动,为了解学生对四种项目的喜欢情况,随机调查了该校m名学生最喜欢的一种项目(每名学生必选且只能选择四种活动项目的一种),并将调查结果绘制成如下的不完整的统计图表:
学生最喜欢的活动项目的人数统计表
项目 | 学生数(名) | 百分比 |
丢沙包 | 20 | 10% |
打篮球 | 60 | p% |
跳大绳 | n | 40% |
踢毽球 | 40 | 20% |
根据图表中提供的信息,解答下列问题:
(1)m= ,n= ,p= ;
(2)请根据以上信息直接补全条形统计图;
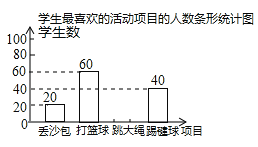
(3)根据抽样调查结果,请你估计该校2000名学生中有多少名学生最喜欢跳大绳.
查看答案和解析>>
科目: 来源: 题型:
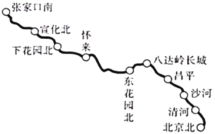
【题目】京张高铁是2022年北京冬奥会的重要交通保障设施.如图,京张高铁起自北京北站,途经清河、沙河、昌平等站,终点站为张家口南站,全长174千米.根据资料显示,京张高铁在某次测试中的平均时速是现运行的京张铁路某![]() 字头列车平均时速的6倍,全程行驶时间减少了122分钟,且每站(不计起始站和终点站)停靠的平均时间也减少了3.5分钟.请求出此次测试中京张高铁的平均时速是多少.
字头列车平均时速的6倍,全程行驶时间减少了122分钟,且每站(不计起始站和终点站)停靠的平均时间也减少了3.5分钟.请求出此次测试中京张高铁的平均时速是多少.
(注:平均时速的测算公式为![]() )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】在![]() 中 ,
中 ,![]() 平分
平分![]() 交
交![]() 于
于![]() ,
,![]() 的两边分别与
的两边分别与![]() ,
, ![]() 相交于
相交于![]() ,
,![]() 两点,且
两点,且![]() .
.
(1)如图,若![]() ,
, ![]() ,
,![]() ,
,![]() ,
,![]() .
.
①写出![]() °,
°,![]() 的长是 .
的长是 .
②求四边形![]() 的周长.
的周长.
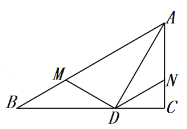
(2)如图,过![]() 作
作![]() 于
于![]() ,作
,作![]() 于
于![]() ,先补全图乙再证明
,先补全图乙再证明![]() .
.

查看答案和解析>>
科目: 来源: 题型:
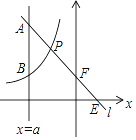
【题目】如图,一次函数y=kx+b的图象l与坐标轴分别交于点E,F,与双曲线y=﹣![]() (x<0)交于点P(﹣1,n),且F是PE的中点,直线x=a与l交于点A,与双曲线交于点B(不同于A),PA=PB,则a=________.
(x<0)交于点P(﹣1,n),且F是PE的中点,直线x=a与l交于点A,与双曲线交于点B(不同于A),PA=PB,则a=________.
查看答案和解析>>
科目: 来源: 题型:
【题目】如果一个分式的分子或分母可以因式分解,且这个分式不可约分,那么我们称这个分式为“和谐分式”.
(1)下列分式中,___________是和谐分式(填写序号即可);
①![]() ; ②
; ②![]() ;③
;③ ![]() ;④
;④ ![]()
(2)若![]() 为整数,且
为整数,且![]() 为和谐分式,请写出
为和谐分式,请写出![]() 的值;
的值;
(3)在化简![]() 时,
时,
小冬和小奥分别进行了如下三步变形:
小冬:原式![]()
小奥:原式![]()
显然,小奥利用了其中的和谐分式, 第三步所得结果比小冬的结果简单,原因是: ,请你接着小奥的方法完成化简.
查看答案和解析>>
科目: 来源: 题型:
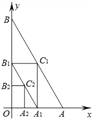
【题目】如图,在平面直角坐标系中,A、B两点分别在x轴和y轴上,OA=1,OB=![]() ,连接AB,过AB中点C1分别作x轴和y轴的垂线,垂足分别是点A1、B1,连接A1B1,再过A1B1中点C2作x轴和y轴的垂线,照此规律依次作下去,则点Cn的坐标为 ___________。
,连接AB,过AB中点C1分别作x轴和y轴的垂线,垂足分别是点A1、B1,连接A1B1,再过A1B1中点C2作x轴和y轴的垂线,照此规律依次作下去,则点Cn的坐标为 ___________。
查看答案和解析>>
科目: 来源: 题型:
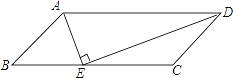
【题目】如图,ABCD中,AE平分∠BAD,交BC于E,DE⊥AE,下列结论::①DE平分∠ADC;②E是BC的中点;③AD=2CD;④梯形ADCE的面积与△ABE的面积比是3:1,其中正确的结论的个数有( )
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目: 来源: 题型:
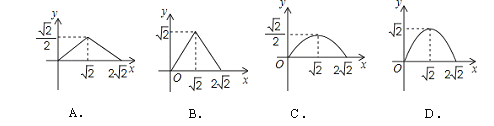
【题目】如图,在矩形ABCD中,AB=2,点E在边AD上,∠ABE=45°,BE=DE,连接BD,点P在线段DE上,过点P作PQ∥BD交BE于点Q,连接QD.设PD=x,△PQD的面积为y,则能表示y与x函数关系的图象大致是( )

查看答案和解析>>
科目: 来源: 题型:
【题目】阅读下面材料:
学习了三角形全等的判定方法(即“SAS”“ASA”“AAS”“SSS”)和直角三角形全等的判定方法(即“HL”)后,小聪继续对“两个三角形满足两边和其中一边的对角对应相等”的情形进行研究
小聪将命题用符号语言表示为:在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E.
小聪的探究方法是对∠B分为“直角、钝角、锐角”三种情况进行探究.
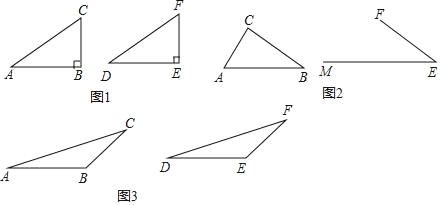
第一种情况:当∠B 是直角时,如图1,△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E=90°,根据“HL”定理,可以知道Rt△ABC≌Rt△DEF.
第二种情况:当∠B 是锐角时,如图2,BC=EF,∠B=∠E<90°,在射线EM上有点D,使DF=AC,画出符合条件的点D,则△ABC和△DEF的关系是 ;
A.全等 B.不全等 C.不一定全等
第三种情况:当∠B是钝角时,如图3,在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E>90°.过点C作AB边的垂线交AB延长线于点M;同理过点F作DE边的垂线交DE延长线于N,根据“ASA”,可以知道△CBM≌△FEN,请补全图形,进而证出△ABC≌△DEF.
查看答案和解析>>
科目: 来源: 题型:
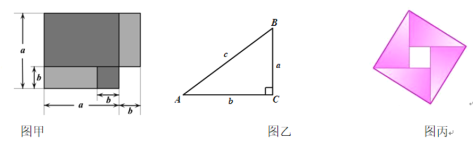
【题目】通过整式乘法的学习,我们进一步了解了利用图形面积来说明法则、公式等的正确性的方法,例如利用图甲可以对平方差公式![]() 给予解释.图乙中的
给予解释.图乙中的![]() 是一个直角三角形,
是一个直角三角形,![]() ,人们很早就发现直角三角形的三边
,人们很早就发现直角三角形的三边![]() 满足
满足![]() 的关系.图丙是2002年国际数学家大会的会徽,选定的是我国古代数学家赵爽用来证明勾股定理的弦图,弦图是由四个全等的直角三角形和中间的小正方形拼成的一个大正方形.如果大正方形的面积是13,小正方形的面积是1,直角三角形的较短直角边长为
的关系.图丙是2002年国际数学家大会的会徽,选定的是我国古代数学家赵爽用来证明勾股定理的弦图,弦图是由四个全等的直角三角形和中间的小正方形拼成的一个大正方形.如果大正方形的面积是13,小正方形的面积是1,直角三角形的较短直角边长为![]() ,较长直角边长为
,较长直角边长为![]() ,求出
,求出![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com