
科目: 来源: 题型:
【题目】如图,在 Rt△ABC 中,∠BAC=90°,AB=6,AC=8,D 为 AC 上一点,将△ABD 沿 BD 折叠,使点 A 恰好落在 BC 上的 E 处,则折痕 BD 的长是( )
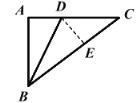
A.5B.![]() C.3
C.3 ![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】在等边![]() 中,线段
中,线段![]() 为
为![]() 边上的中线.动点
边上的中线.动点![]() 在直线
在直线![]() 上时,以
上时,以![]() 为一边在
为一边在![]() 的下方作等边
的下方作等边![]() ,连结BE.
,连结BE.
(1)若点![]() 在线段
在线段![]() 上时(如图),则
上时(如图),则![]()
![]() (填“>”、“<”或“=”),
(填“>”、“<”或“=”),![]() 度;
度;

(2)设直线BE与直线![]() 的交点为O.
的交点为O.
①当动点![]() 在线段
在线段![]() 的延长线上时(如图),试判断
的延长线上时(如图),试判断![]() 与
与![]() 的数量关系,并说明理由;
的数量关系,并说明理由;


②当动点![]() 在直线
在直线![]() 上时,试判断
上时,试判断![]() 是否为定值?若是,请直接写出
是否为定值?若是,请直接写出![]() 的度数;若不是,请说明理由.
的度数;若不是,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某公司计划购买![]() 、
、![]() 两种型号的机器人搬运材料,已知
两种型号的机器人搬运材料,已知![]() 型机器人比
型机器人比![]() 型机器人每小时多搬运
型机器人每小时多搬运![]() 材料,且
材料,且![]() 型机器人搬运
型机器人搬运![]() 的材料所用的时间与
的材料所用的时间与![]() 型机器人搬运
型机器人搬运![]() 材料所用的时间相同.
材料所用的时间相同.
(1)求![]() 、
、![]() 两种型号的机器人每小时分别搬运多少材料?
两种型号的机器人每小时分别搬运多少材料?
(2)该公司计划采购![]() 、
、![]() 两种型号的机器人共
两种型号的机器人共![]() 台,要求每小时搬运的材料不得少于
台,要求每小时搬运的材料不得少于![]() ,则至少购进
,则至少购进![]() 型机器人多少台?
型机器人多少台?
查看答案和解析>>
科目: 来源: 题型:
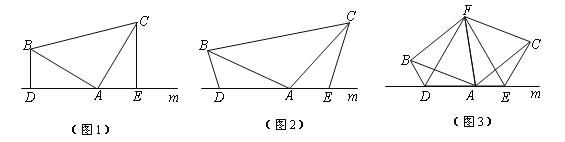
【题目】(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m, CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.
(2) 如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=![]() ,其中
,其中![]() 为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
(3)拓展与应用:如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状.
查看答案和解析>>
科目: 来源: 题型:
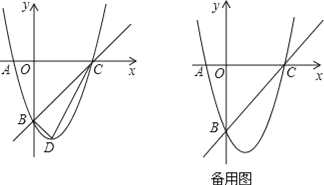
【题目】已知,m,n是一元二次方程x2+4x+3=0的两个实数根,且|m|<|n|,抛物线y=x2+bx+c的图象经过点A(m,0),B(0,n),如图所示.
(1)求这个抛物线的解析式;
(2)设(1)中的抛物线与x轴的另一个交点为抛物线的顶点为D,求出点C,D的坐标,并判断△BCD的形状;
(3)点P是直线BC上的一个动点(点P不与点B和点C重合),过点P作x轴的垂线,交抛物线于点M,点Q在直线BC上,距离点P为![]() 个单位长度,设点P的横坐标为t,△PMQ的面积为S,求出S与t之间的函数关系式.
个单位长度,设点P的横坐标为t,△PMQ的面积为S,求出S与t之间的函数关系式.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知等腰三角形ABC中,AB=AC,点D、E分别在边AB、AC上,且AD=AE,连接BE、CD,交于点F.
(1)判断∠ABE与∠ACD的数量关系,并说明理由;
(2)求证:过点A、F的直线垂直平分线段BC.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,AB是⊙O的直径,弦DE垂直平分半径OA,C为垂足,弦DF与半径OB相交于点P,连结EF、EO,若DE=![]() ,∠DPA=45°.
,∠DPA=45°.
(1)求⊙O的半径;
(2)求图中阴影部分的面积.

查看答案和解析>>
科目: 来源: 题型:
【题目】某小学学生较多,为了便于学生尽快就餐,师生约定:早餐一人一份,一份两样,一样一个,食堂师傅在窗口随机发放(发放的食品价格一样),食堂在某天早餐提供了猪肉包、面包、鸡蛋、油饼四样食品.
(1)按约定,“小李同学在该天早餐得到两个油饼”是 事件;(可能,必然,不可能)
(2)请用列表或树状图的方法,求出小张同学该天早餐刚好得到猪肉包和油饼的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】用A、B两种机器人搬运大米,A型机器人比B型机器人每小时多搬运20袋大米,A型机器人搬运700袋大米与B型机器人搬运500袋大米所用时间相等.求A、B型机器人每小时分别搬运多少袋大米.
查看答案和解析>>
科目: 来源: 题型:
【题目】现代互联网技术的广泛应用,催生了快递行业的高速发展.阜阳市某家快递公司,2017年3月份与5月份完成投递的快递总件数分别为10万件和12.1万件.现假定该公司每月投递的快递总件数的增长率相同.
(1)求该快递公司投递快递总件数的月平均增长率?
(2) 如果平均每人每月最多可投递快递0.6万件,那么该公司现有的21名快递投递业务员能否完成2017年6月份的快递投递任务?如果不能,请问至少需要增加几名业务员?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com