
科目: 来源: 题型:
【题目】下面是“求作∠AOB的角平分线”的尺规作图过程.

已知:如图,钝角∠AOB.求作:∠AOB的角平分线.
作法:

①在OA和OB上,分别截取OD、OE,使OD=OE;
②分别以D、E为圆心,大于![]() 的长为半径作弧,在∠AOB内,两弧交于点C;
的长为半径作弧,在∠AOB内,两弧交于点C;
③作射线OC.
所以射线OC就是所求作的∠AOB的角平分线.
在该作图中蕴含着几何的证明过程:
由①可得:OD=OE
由②可得:_________________
由③可知:OC=OC
∴______≌_________(依据:________________________)
∴可得∠COD=∠COE(全等三角形对应角相等)
即OC就是所求作的∠AOB的角平分线.
查看答案和解析>>
科目: 来源: 题型:
【题目】某店只销售某种进价为40元/kg的产品,已知该店按60元kg出售时,每天可售出100kg,后来经过市场调查发现,单价每降低1元,则每天的销售量可增加10kg.
(1)若单价降低2元,则每天的销售量是_____千克,每天的利润为_____元;若单价降低x元,则每天的销售量是_____千克,每天的利润为______元;(用含x的代数式表示)
(2)若该店销售这种产品计划每天获利2240元,单价应降价多少元?
(3)当单价降低多少元时,该店每天的利润最大,最大利润是多少元?
查看答案和解析>>
科目: 来源: 题型:
【题目】规定:[m]为不大于m的最大整数;
(1)填空:[3.2]= ,[-4.8]= ;
(2)已知:动点C在数轴上表示数a,且-2≤[a]≤4,则a的取值范围;
(3)求方程4x-3[x]+5=0的整数解.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴为x=![]() ,且经过点(2,0),下列说法:①abc<0;②﹣2b+c=0;③4a+2b+c<0;④若(
,且经过点(2,0),下列说法:①abc<0;②﹣2b+c=0;③4a+2b+c<0;④若(![]() ,y1)、(
,y1)、(![]() ,y2)是抛物线上的两点,则y1<y2;⑤
,y2)是抛物线上的两点,则y1<y2;⑤![]() >m(am+b)(其中m≠
>m(am+b)(其中m≠![]() ).其中说法正确的是_____
).其中说法正确的是_____

查看答案和解析>>
科目: 来源: 题型:
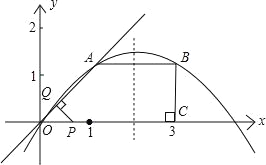
【题目】如图所示,已知在直角梯形OABC中,AB∥OC,BC⊥x轴于点C、A(1,1)、B(3,1).动点P从O点出发,沿x轴正方向以每秒1个单位长度的速度移动.过P点作PQ垂直于直线OA,垂足为Q.设P点移动的时间为t秒(0<t<4),△OPQ与直角梯形OABC重叠部分的面积为S.
(1)求经过O、A、B三点的抛物线解析式;
(2)求S与t的函数关系式;
(3)将△OPQ绕着点P顺时针旋转90°,是否存在t,使得△OPQ的顶点O或Q在抛物线上?若存在,直接写出t的值;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,点A在直线l上,点B在直线l外,点B关于直线l的对称点为C,连接AC,过点B作BD⊥AC于点D,延长BD至E使BE=AB,连接AE并延长与BC的延长线交于点F.

(1)补全图形;
(2)若∠BAC=2α,求出∠AEB的大小(用含α的式子表示);
(3)用等式表示线段EF与BC的数量关系,并证明.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知∠MAN=30°,点B在射线AM上,且 AB=6,点C在射线AN上.

(1)若△ABC是直角三角形,求AC的长;
(2)若△ABC是等腰三角形,则满足条件的C点有 个;
(3)设BC=x,当△ABC唯一确定时, 直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】小明与小志要到延庆冬奥综合训练馆参加滑冰训练,他们约定从德胜门出发自驾前往,但他们在选择路线时产生了分歧.根据导航提示小明选择方案1前往,小志选择方案2前往,由于方案1比方案2的路线长,而小明还想大家一起到达.已知小明的平均车速比小志的平均车速每小时快8千米,请你帮助小明算一算,他的平均车速为每小时多少千米,他们就可以同时到达?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com