
科目: 来源: 题型:
【题目】如图,正方形ABCD与正方形A1B1C1D1关于某点中心对称,已知A, D1,D三点的坐标分别是(0,4),(0,3),(0,2).

(1)对称中心的坐标;
(2)写出顶点B, C, B1 , C1的坐标.
查看答案和解析>>
科目: 来源: 题型:
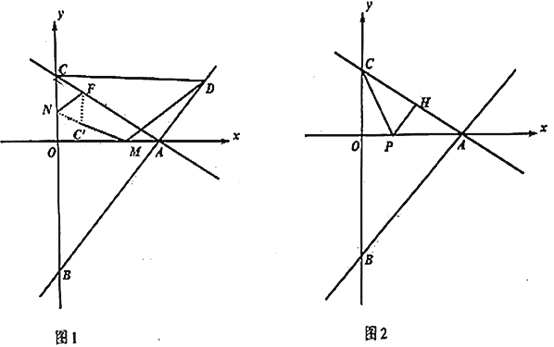
【题目】如图1,已知直线![]() 和直线
和直线![]() 交于
交于![]() 轴上一点
轴上一点![]() ,且分别交
,且分别交![]() 轴于点
轴于点![]() 、点
、点![]() ,且
,且![]() .
.
(1)求![]() 的值;
的值;
(2)如图1,点![]() 是直线
是直线![]() 上一点,且在
上一点,且在![]() 轴上方,当
轴上方,当![]() 时,在线段
时,在线段![]() 上取一点
上取一点![]() ,使得
,使得![]() ,点
,点![]() 分别为
分别为![]() 轴、
轴、![]() 轴上的动点,连接
轴上的动点,连接![]() ,将
,将![]() 沿
沿![]() 翻折至
翻折至![]() ,求
,求![]() 的最小值;
的最小值;
(3)如图2,![]() 分别为射线
分别为射线![]() 上的动点,连接
上的动点,连接![]() 是否存在这样的点
是否存在这样的点![]() ,使得
,使得![]() 为等腰三角形,
为等腰三角形,![]() 为直角三角形同时成立.请直接写出满足条件的点
为直角三角形同时成立.请直接写出满足条件的点![]() 坐标.
坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知点A(2,3)和直线y=x,
(1)点A关于直线y=x的对称点为点B,点A关于原点(0,0)的对称点为点C;写出点B、C的坐标;
(2)若点D是点B关于原点(0,0)的对称点,判断四形ABCD的形状,并说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】今年受猪瘟影响,从年初开始,猪肉价格不断走高.消费者王阿姨发现,9月20日当天猪肉的价格是年初的1.5倍;9月20日当天,王阿姨购买4千克猪肉比年初多花了48元.
(1)那么9月20日当天猪肉的价格为每千克多少元?
(2)9月20日,按照(1)中的猪肉价格,某售卖点共卖出1000千克猪肉.9月21日,政府决定投入储备猪肉并规定其销售价在9月20日的基础上下调![]() 出售.该焦卖点按规定价出售一批储备猪肉和非储备猪肉,该售卖点的非储备猪肉仍按9月20日的价格出售,9月21日当天的两种猪肉总销量比9月20日增加了20%,且储备猪肉的销量占总销量的
出售.该焦卖点按规定价出售一批储备猪肉和非储备猪肉,该售卖点的非储备猪肉仍按9月20日的价格出售,9月21日当天的两种猪肉总销量比9月20日增加了20%,且储备猪肉的销量占总销量的![]() ,两种猪肉销售的总金额比9月20日至少提高了
,两种猪肉销售的总金额比9月20日至少提高了![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目: 来源: 题型:
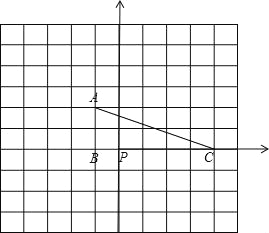
【题目】如图,△ABC中任意一点P(xo,yo),将△ABC平移后得到△A1B1C1,点P的对应点P1(xo+6,yo+4).
(1)写出A1、B1、C1的坐标.
(2)若三角形外有一点M经过同样的平移后得到点N(5,3),写出M点关于原点对称的点的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】有这样一个问题:探究函数![]() 的图象与性质.
的图象与性质.
小东根据学习函数的经验,对函数![]() 的图象与性质进行了探究.
的图象与性质进行了探究.
下面是小东的探究过程,请补充完成:
(1)化简函数解析式,当x≥-1时,y= ,当x<-1时y= ;
(2)根据(1)中的结果,请在所给坐标系中画出函数![]() 的图象;
的图象;
(3)结合函数图象,写出该函数的一条性质: .
(4)结合画出的函数图象,解决问题:若关于x的方程![]() 只有一个实数根,直接写出实数a的取值范围: .
只有一个实数根,直接写出实数a的取值范围: .

查看答案和解析>>
科目: 来源: 题型:
【题目】为了绿化环境,巴蜀中学七年级一班同学都积极参加了植树活动.去年4月份该班同学的植树情况的部分统计如下图所示:
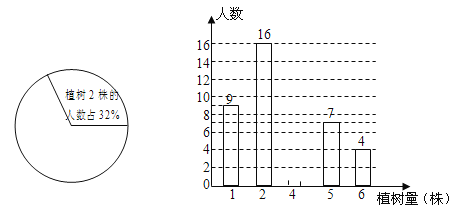
(1)根据以上统计图中的信息,
①该班有_____人;②植树株数的中位数是__________株;
③该班植树为5株的人数占该班总人数的百分比________________.
(2)请将该条形统计图补充完整;
(3)据统计,全年级每班植树情况大致相同,请根据该班的植树情况,估计全年级2000人中植树大于4棵的一共有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com