
科目: 来源: 题型:
【题目】如图,AB是⊙O的一条弦,点C是⊙O上一动点,且∠ACB=30°,点E,F分别是AC,BC的中点,直线EF与⊙O交于G,H两点,若⊙O的半径为6,则GE+FH的最大值为( )
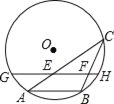
A. 6 B. 9 C. 10 D. 12
查看答案和解析>>
科目: 来源: 题型:
【题目】甲乙两位老师同住一小区,该小区与学校相距![]() 米.甲从小区步行去学校,出发
米.甲从小区步行去学校,出发![]() 分钟后乙再出发,乙从小区先骑公共自行车,骑行若干米到达还车点后,立即步行走到学校.已知乙骑车的速度为
分钟后乙再出发,乙从小区先骑公共自行车,骑行若干米到达还车点后,立即步行走到学校.已知乙骑车的速度为![]() 米/分,甲步行的速度比乙步行的速度每分钟快
米/分,甲步行的速度比乙步行的速度每分钟快![]() 米.设甲步行的时间为
米.设甲步行的时间为![]() (分),图1中线段
(分),图1中线段![]() 与折线
与折线![]() 分别表示甲、乙离小区的路程
分别表示甲、乙离小区的路程![]() (米)与甲步行时间
(米)与甲步行时间![]() (分)的函数关系的图象;图2表示甲、乙两人之间的距离
(分)的函数关系的图象;图2表示甲、乙两人之间的距离![]() (米)与甲步行时间
(米)与甲步行时间![]() (分)的函数关系的图象(不完整),根据图1和图2中所给的信息,解答下列问题:
(分)的函数关系的图象(不完整),根据图1和图2中所给的信息,解答下列问题:


(1)求甲步行的速度和乙出发时甲离开小区的路程;
(2)求直线![]() 的解析式;
的解析式;
(3)在图2中,画出当![]() 时,
时,![]() 关于
关于![]() 的函数的大致图象.
的函数的大致图象.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,抛物线y=﹣![]() x2+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).
x2+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).
(1)求抛物线的表达式;
(2)在抛物线的对称轴上是否存在点P,使△PCD是以CD为腰的等腰三角形?如果存在,直接写出P点的坐标;如果不存在,请说明理由;
(3)点E时线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,四边形CDBF的面积最大?求出四边形CDBF的最大面积及此时E点的坐标.

查看答案和解析>>
科目: 来源: 题型:
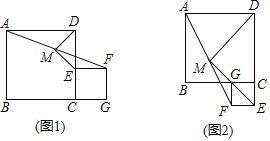
【题目】已知正方形ABCD与正方形CEFG,M是AF的中点,连接DM,EM.
(1)如图1,点E在CD上,点G在BC的延长线上,请判断DM,EM的数量关系与位置关系,并直接写出结论;
(2)如图2,点E在DC的延长线上,点G在BC上,(1)中结论是否仍然成立?请证明你的结论;
(3)将图1中的正方形CEFG绕点C旋转,使D,E,F三点在一条直线上,若AB=13,CE=5,请画出图形,并直接写出MF的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△AOB中,OA=OB,点C为AB的中点,AB=16,以点O为圈心,6为半径的圆经过点C,分别交OA、OB于点E、F.
(1)求证:AB为⊙O的切线;
(2)求图中阴影部分的面积.(注:结果保留π,sin37°=0.6,cos37°=0.8,tan37°=0.75)

查看答案和解析>>
科目: 来源: 题型:
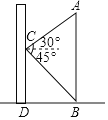
【题目】如图,在数学活动课上,小丽为了测量校园内旗杆AB的高度,站在教学楼的C处测得旗杆底端B的俯角为45°,测得旗杆顶端A的仰角为30°.已知旗杆与教学楼的距离BD=9m,请你帮她求出旗杆的高度(结果保留根号).
查看答案和解析>>
科目: 来源: 题型:
【题目】某网络约车公司近期推出了“520专享”服务计划,即要求公司员工做到“5星级服务、2分钟响应、0客户投诉”,为进一步提升服务品质,公司监管部门决定了解“单次营运里程”的分布情况.老王收集了本公司的5 000个“单次营运里程”数据,这些里程数据均不超过25(公里),他从中随机抽取了200个数据作为一个样本,整理、统计结果如下表,并绘制了不完整的频数分布直方图.
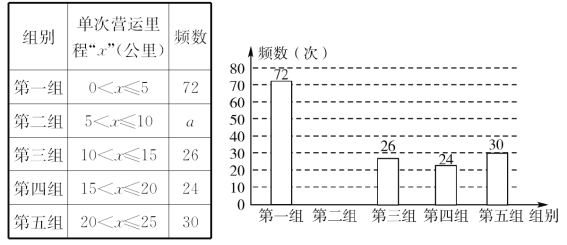
根据统计表、图提供的信息,解答下面的问题:
(1)表中a=________;样本中“单次营运里程”不超过15公里的频率为________;(2)请把频数分布直方图补充完整;
(3)请估计该公司这5 000个“单次营运里程”超过20公里的次数;
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,点D,E,F分别是△ABC三边的中点,则下列判断错误的是( )

A. 四边形AEDF一定是平行四边形 B. 若AD平分∠A,则四边形AEDF是正方形
C. 若AD⊥BC,则四边形AEDF是菱形 D. 若∠A=90°,则四边形AEDF是矩形
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,⊙P经过x轴上一点C,与y轴分别相交于A、B两点,连接AP并延长分别交⊙P、x轴于点D、点E,连接DC并延长交y轴于点F ,且DC=FC,点D的坐标为(12,-2).
(1)判断⊙P与x轴的位置关系,并说明理由;
(2)求⊙P半径;
(3)若弧BD上有一动点M,连接AM,过B点作BN⊥AM,垂足为N,连DN,则DN的最小值是 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com