
科目: 来源: 题型:
【题目】小左同学想利用影长测量学校旗杆的高度,如图,她在某一时刻立一长度为1米的标杆,测得其影长为![]() 米,同时旗杆投影的一部分在地上,另一部分在某一建筑物的墙上,测得旗杆与建筑物的距离为10米,旗杆在墙上的影高为2米,请帮小左同学算出学校旗杆的高度.
米,同时旗杆投影的一部分在地上,另一部分在某一建筑物的墙上,测得旗杆与建筑物的距离为10米,旗杆在墙上的影高为2米,请帮小左同学算出学校旗杆的高度.

查看答案和解析>>
科目: 来源: 题型:
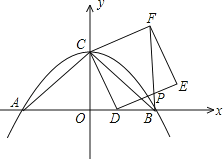
【题目】如图,抛物线y=﹣![]() x2+4交x轴于点A、B,交y轴于点C,连结AC,BC,D是线段OB上一动点,以CD为一边向右侧作正方形CDEF,连结BF,交DE于点P.
x2+4交x轴于点A、B,交y轴于点C,连结AC,BC,D是线段OB上一动点,以CD为一边向右侧作正方形CDEF,连结BF,交DE于点P.
(1)试判断△ABC的形状,并说明理由;
(2)求证:BF⊥AB.
(3)当点D从点O沿x轴正方向移动到点B时,点E所走过的路线长为______;
(4)探究当点D在何处时,△FBC是等腰三角形,并求出相应的BF的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,二次函数y=(x﹣3)2+m的图象与y轴交于点C,点B是点C关于该二次函数图象的对称轴对称的点,已知一次函数y=kx+b的图象经过该二次函数图象上的点A(1,0)及点B.
(1)求二次函数与一次函数的解析式;
(2)抛物线上是否存在一点P,使S△ABP=S△ABC?若存在,请求出点P的坐标,若不存在,请说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】草莓是云南多地盛产的一种水果,今年某水果销售店在草莓销售旺季,试销售成本为每千克![]() 元的草莓,规定试销期间销售单价不低于成本单价,也不高于每千克
元的草莓,规定试销期间销售单价不低于成本单价,也不高于每千克![]() 元,经试销发现,销售量
元,经试销发现,销售量![]() (千克)与销售单价
(千克)与销售单价![]() (元)符合一次函数关系,如图是
(元)符合一次函数关系,如图是![]() 与
与![]() 的函数关系图象.
的函数关系图象.

![]() 求
求![]() 与
与![]() 的函数解析式(也称关系式);
的函数解析式(也称关系式);
![]() 设该水果销售店试销草莓获得的利润为
设该水果销售店试销草莓获得的利润为![]() 元,求
元,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目: 来源: 题型:
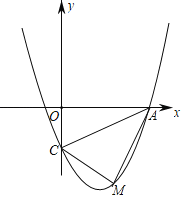
【题目】如图,抛物线经过点A(4,0)、B(﹣2,0)、C(0,﹣4)
(1)求抛物线的解析式;
(2)在抛物线AC段上是否存在点M,使△ACM的面积为3,求出在此时M的坐标,若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
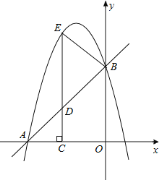
【题目】如图,在平面直角坐标系![]() 中,直线
中,直线![]() 与坐标轴分别交于
与坐标轴分别交于![]() 、
、![]() 两点,抛物线
两点,抛物线![]() 过
过![]() 、
、![]() 两点,点
两点,点![]() 为线段
为线段![]() 上一动点,过点
上一动点,过点![]() 作
作![]() 轴于点
轴于点![]() ,交抛物线于点
,交抛物线于点![]() .
.
![]() 求抛物线的解析式.
求抛物线的解析式.
![]() 求
求![]() 面积的最大值.
面积的最大值.
![]() 连接
连接![]() ,是否存在点
,是否存在点![]() ,使得
,使得![]() 和
和![]() 相似?若存在,求出点
相似?若存在,求出点![]() 坐标;若不存在,说明理由.
坐标;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com