
科目: 来源: 题型:
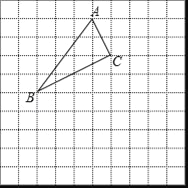
【题目】如图,△ABC在正方形网格中,若A(0,3),按要求回答下列问题
(1)在图中建立正确的平面直角坐标系;
(2)根据所建立的坐标系,写出B和C的坐标;
(3)计算△ABC的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点D在△ABC内,BD=BC,∠DBC=60°,点E在△ABC外,∠BCE=150°,∠ABE=60°.
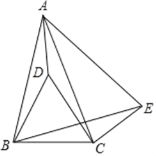
(1)求证:△ADB≌△ADC , 并求出∠ADB的度数;
(2)小明说△ABE是等腰三角形,小华说△ABE是等边三角形.请问 说法更准确,并说明理由.
(3)连接DE,若DE⊥BD,DE=8,求AD的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】某一工程,在工程招标时,接到甲、乙两个工程队的投标书.施工一天,需付甲工程队工程款1.2万元,乙工程队工程款0.5万元.工程领导小组根据甲、乙两队的投标书测算,有如下方案:
(1)甲队单独完成这项工程刚好如期完成;
(2)乙队单独完成这项工程要比规定日期多用6天;
(3)若甲、乙两队合作3天,余下的工程由乙队单独做也正好如期完成.
试问:(1)规定日期是多少天?
(2)在不耽误工期的前提下,你觉得哪一种施工方案最节省工程款?请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】把几个图形拼成一个新的图形,再通过图形面积的计算,常常可以得到一些有用的式子,或可以求出一些不规则图形的面积.
(1)选择题:图1是一个长2a、宽2b(a>b)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形.然后,按图2那样拼成一个(中间空的)正方形,则中间空的部分面积是( )
A.2ab B.(a+b)2 C.(a﹣b)2 D.a2﹣b2
(2)如图3,是将几个面积不等的小正方形与小长方形拼成一个边长为a+b+c的正方形,试用不同的方法计算这个图形的面积.据此,你能发现什么结论,请直接写出来:
(3)如图4,是将两个边长分别为a和b的正方形拼在一起,B、C、G三点在同一直线上,连接BD和BF.若两个正方形的边长满足a+b=10,ab=20,求阴影部分的面积.


查看答案和解析>>
科目: 来源: 题型:
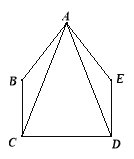
【题目】(本题8分)如图,在五边形ABCDE中,∠BCD=∠EDC=90°,BC=ED,AC=AD.
(1)求证:△ABC≌△AED;
(2)当∠B=140°时,求∠BAE的度数.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,△ABC中,AD是∠BAC的角平分线,若AB=AC+CD.那么∠ACB 与∠ABC有怎样的数量关系? 小明通过观察分析,形成了如下解题思路:


如图2,延长AC到E,使CE=CD,连接DE,由AB=AC+CD,可得AE=AB,又因为AD是∠BAC的平分线,可得△ABD≌△AED,进一步分析就可以得到∠ACB 与∠ABC的数量关系.
(1) 判定△ABD 与△AED 全等的依据是______________(SSS,SAS,ASA,AAS 从其中选择一个);
(2)∠ACB 与∠ABC的数量关系为:___________________
查看答案和解析>>
科目: 来源: 题型:
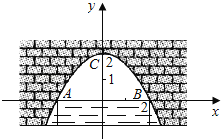
【题目】图中是抛物线形拱桥,当拱顶离水面2m时,水面宽4m,建立如图所示的平面直角坐标系:
(1)求拱桥所在抛物线的解析式;
(2)当水面下降1m时,则水面的宽度为多少?
查看答案和解析>>
科目: 来源: 题型:
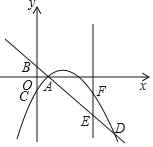
【题目】如图,在平面直角坐标系中,直线y=﹣x+2交x轴于点A,交y轴于点B,过点A的抛物线y=ax2+bx﹣2与y轴交点C,与直线AB的另一个交点为D,点E是线段AD上一点,点F在抛物线上,EF∥y轴,设E的横坐标为m
(1)用含a的代数式表示b.
(2)当点D的横坐标为8时,求出a的值.
(3)在(2)的条件下,设△ABF的面积为S,求出S最大值,并求出此时m的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图平面直角坐标系中,A点坐标为(0,1),AB=BC=![]() ,∠ABC=90°,CD⊥x轴.
,∠ABC=90°,CD⊥x轴.
(1)填空:B点坐标为 ,C点坐标为 .
(2)若点P是直线CD上第一象限上一点且△PAB的面积为6.5,求P点的坐标;
(3)在(2)的条件下点M是x轴上线段OD之间的一动点,当△PAM为等腰三角形时,直接写出点M的坐标.

查看答案和解析>>
科目: 来源: 题型:
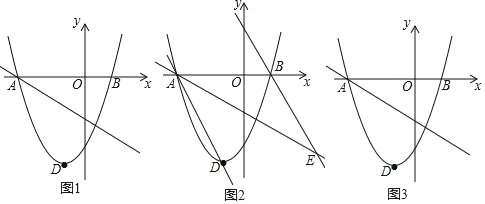
【题目】如图1,已知二次函数y=mx2+3mx﹣![]() m的图象与x轴交于A,B两点(点A在点B的左侧),顶点D和点B关于过点A的直线l:y=﹣
m的图象与x轴交于A,B两点(点A在点B的左侧),顶点D和点B关于过点A的直线l:y=﹣![]() x﹣
x﹣![]() 对称.
对称.
(1)求A、B两点的坐标及二次函数解析式;
(2)如图2,作直线AD,过点B作AD的平行线交直线1于点E,若点P是直线AD上的一动点,点Q是直线AE上的一动点.连接DQ、QP、PE,试求DQ+QP+PE的最小值;若不存在,请说明理由:
(3)将二次函数图象向右平移![]() 个单位,再向上平移3
个单位,再向上平移3![]() 个单位,平移后的二次函数图象上存在一点M,其横坐标为3,在y轴上是否存在点F,使得∠MAF=45°?若存在,请求出点F坐标;若不存在,请说明理由.
个单位,平移后的二次函数图象上存在一点M,其横坐标为3,在y轴上是否存在点F,使得∠MAF=45°?若存在,请求出点F坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com