
科目: 来源: 题型:
【题目】如图,Rt△ABO的顶点A是反比例函数y=![]() 的图象与一次函数y=-x-(k+1)的图象在第二象限的交点,AB⊥x轴于点B,且S△ABO=
的图象与一次函数y=-x-(k+1)的图象在第二象限的交点,AB⊥x轴于点B,且S△ABO=![]() .
.

(1)求反比例函数和一次函数的解析式;
(2)求一次函数与反比例函数图象的两个交点A,C的坐标以及△AOC的面积;
(3)当x为何值时,一次函数的值大于反比例函数的值.
查看答案和解析>>
科目: 来源: 题型:
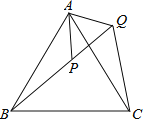
【题目】在等边三角形ABC中,点P在△ABC内,点Q在△ABC外,且∠ABP=∠ACQ,BP=CQ.
(1)求证:△ABP≌△ACQ;
(2)请判断△APQ是什么三角形,试说明你的结论.
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读下面材料,并解答问题.
材料:将分式![]() 拆分成一个整式与一个分式(分子为整数)的和的形式.
拆分成一个整式与一个分式(分子为整数)的和的形式.
解析:
由分母为![]() ,可设
,可设![]()
则![]()
![]() 对应任意x,上述等式均成立,
对应任意x,上述等式均成立,![]() ,
,![]() ,
,![]() .
.
![]() .
.
这样,分式![]() 被拆分成了一个整式
被拆分成了一个整式![]() 与一个分式
与一个分式![]() 的和.
的和.
解答:
(1)将分式![]() 拆分成一个整式与一个分式(分子为整数)的和的形式.
拆分成一个整式与一个分式(分子为整数)的和的形式.
(2)当![]() 时,直接写出
时,直接写出![]() ________,
________,![]() 的最小值为________.
的最小值为________.
查看答案和解析>>
科目: 来源: 题型:
【题目】某县为了落实中央的“强基惠民工程”,计划将某村的居民自来水管道进行改造.该工程若由甲队单独施工恰好在规定时间内完成;若乙队单独施工,则完成工程所需天数是规定天数的1.5倍.如果由甲、乙队先合做15天,那么余下的工程由甲队单独完成还需5天.
(1)这项工程的规定时间是多少天?
(2)已知甲队每天的施工费用为6500元,乙队每天的施工费用为3500元.为了缩短工期以减少对居民用水的影响,工程指挥部最终决定该工程由甲、乙队合做来完成.则该工程施工费用是多少?
查看答案和解析>>
科目: 来源: 题型:
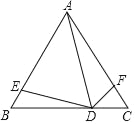
【题目】如图,△ABC是等边三角形,点D是BC边上一动点,点E,F分别在AB,AC边上,连接AD,DE,DF,且∠ADE=∠ADF=60°.
小明通过观察、实验,提出猜想:在点D运动的过程中,始终有AE=AF,小明把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的几种想法:
想法1:利用AD是∠EDF的角平分线,构造△ADF的全等三角形,然后通过等腰三角形的相关知识获证.
想法2:利用AD是∠EDF的角平分线,构造角平分线的性质定理的基本图形,然后通过全等三角形的相关知识获证.
想法3:将△ACD绕点A顺时针旋转至△ABG,使得AC和AB重合,然后通过全等三角形的相关知识获证.
请你参考上面的想法,帮助小明证明AE=AF.(一种方法即可)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知![]() 中,
中,![]() 厘米,
厘米,![]() 厘米,点
厘米,点![]() 为
为![]() 的中点.
的中点.

(1)如果点P在线段BC上以3厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.
①若点Q的运动速度与点P的运动速度相等,经过1秒后,![]() 与
与![]() 是否全等,请说明理由;
是否全等,请说明理由;
②若点Q的运动速度与点P的运动速度不相等, ![]() 与
与![]() 是否可能全等?若能,求出全等时点Q的运动速度和时间;若不能,请说明理由.
是否可能全等?若能,求出全等时点Q的运动速度和时间;若不能,请说明理由.
(2)若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿![]() 三边运动,求经过多长时间点P与点Q第一次在
三边运动,求经过多长时间点P与点Q第一次在![]() 的哪条边上相遇?
的哪条边上相遇?
查看答案和解析>>
科目: 来源: 题型:
【题目】已知,在![]() 中,
中,![]() ,点
,点![]() 为
为![]() 的中点.
的中点.
(1)观察猜想:如图①,若点![]() 、
、![]() 分别为
分别为![]() 、
、![]() 上的点,且
上的点,且![]() 于点
于点![]() ,则线段
,则线段![]() 与
与![]() 的数量关系是_______;(不说明理由)
的数量关系是_______;(不说明理由)
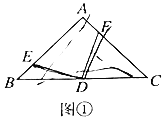
(2)类比探究:若点![]() 、
、![]() 分别为
分别为![]() 、
、![]() 延长线上的点,且
延长线上的点,且![]() 于点
于点![]() ,请写出
,请写出![]() 与
与![]() 的数量关系,在图②中画出符合题意的图形,并说明理由;
的数量关系,在图②中画出符合题意的图形,并说明理由;

(3)解决问题:如图③,点![]() 在
在![]() 的延长线上,点
的延长线上,点![]() 在
在![]() 上,且
上,且![]() ,若
,若![]() ,求
,求![]() 的长.(直接写出结果,不说明理由.)
的长.(直接写出结果,不说明理由.)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com