
科目: 来源: 题型:
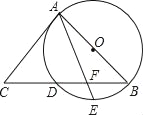
【题目】如图,AB是⊙O的直径,BC交⊙O于点D,E是![]() 的中点,AE与BC交于点F,∠C=2∠EAB.
的中点,AE与BC交于点F,∠C=2∠EAB.
(1)求证:AC是⊙O的切线;
(2)已知CD=4,CA=6,
①求CB的长;
②求DF的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】我们定义:两边平方和等于第三边平方的2倍的三角形叫做奇异三角形.
例如:某三角形三边长分别是2,4,![]() ,因为
,因为![]() ,所以这个三角形是奇异三角形.
,所以这个三角形是奇异三角形.
(1)根据定义:“等边三角形是奇异三角形”这个命题是______命题(填“真”或“假命题”);
(2)在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,且
,且![]() ,若
,若![]() 是奇异三角形,求
是奇异三角形,求![]() ;
;
(3)如图,以![]() 为斜边分别在
为斜边分别在![]() 的两侧作直角三角形,且
的两侧作直角三角形,且![]() ,若四边形
,若四边形![]() 内存在点
内存在点![]() ,使得
,使得![]() ,
,![]() .
.
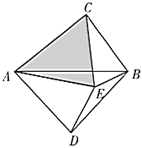
①求证:![]() 是奇异三角形;
是奇异三角形;
②当![]() 是直角三角形时,求
是直角三角形时,求![]() 的度数.
的度数.
查看答案和解析>>
科目: 来源: 题型:
【题目】今年,长沙开始推广垃圾分类,分类垃圾桶成为我们生活中的必备工具.某学校开学初购进![]() 型和
型和![]() 型两种分类垃圾桶,购买
型两种分类垃圾桶,购买![]() 型垃圾桶花费了2500元,购买
型垃圾桶花费了2500元,购买![]() 型垃圾桶花费了2000元,且购买
型垃圾桶花费了2000元,且购买![]() 型垃圾桶数量是购买
型垃圾桶数量是购买![]() 型垃圾桶数量的2倍,已知购买一个
型垃圾桶数量的2倍,已知购买一个![]() 型垃圾桶比购买一个
型垃圾桶比购买一个![]() 型垃圾桶多花30元.
型垃圾桶多花30元.
(1)求购买一个![]() 型垃圾桶、B型垃圾桶各需多少元?
型垃圾桶、B型垃圾桶各需多少元?
(2)由于实际需要,学校决定再次购买分类垃圾桶,已知此次购进![]() 型和
型和![]() 型两种分类垃圾桶的数量一共为50个,恰逢市场对这两种垃圾桶的售价进行调整,
型两种分类垃圾桶的数量一共为50个,恰逢市场对这两种垃圾桶的售价进行调整,![]() 型垃圾桶售价比第一次购买时提高了8%,
型垃圾桶售价比第一次购买时提高了8%,![]() 型垃圾桶按第一次购买时售价的9折出售,如果此次购买
型垃圾桶按第一次购买时售价的9折出售,如果此次购买![]() 型和
型和![]() 型这两种垃圾桶的总费用不超过3240元,那么此次最多可购买多少个
型这两种垃圾桶的总费用不超过3240元,那么此次最多可购买多少个![]() 型垃圾桶?
型垃圾桶?
查看答案和解析>>
科目: 来源: 题型:
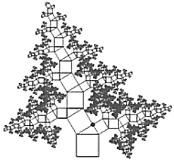
【题目】勾股定理揭示了直角三角形三边之间的关系,其中蕴含着丰富的科学知识和人文价值.如图所示,是一棵由正方形和含![]() 角的直角三角形按一定规律长成的勾股树,树的主干自下而上第一个正方形和第一个直角三角形的面积之和为
角的直角三角形按一定规律长成的勾股树,树的主干自下而上第一个正方形和第一个直角三角形的面积之和为![]() ,第二个正方形和第二个直角三角形的面积之和为
,第二个正方形和第二个直角三角形的面积之和为![]() ,…,第
,…,第![]() 个正方形和第
个正方形和第![]() 个直角三角形的面积之和为
个直角三角形的面积之和为![]() .
.
设第一个正方形的边长为1.
请解答下列问题:
(1)![]() ______.
______.
(2)通过探究,用含![]() 的代数式表示
的代数式表示![]() ,则
,则![]() ______.
______.
查看答案和解析>>
科目: 来源: 题型:
【题目】设![]() ,
,![]() 是实数,定义关于“*”的一种运算:
是实数,定义关于“*”的一种运算:![]() .则下列结论正确的是( )
.则下列结论正确的是( )
①若![]() ,则
,则![]() 或
或![]() ;
;
②不存在实数![]() ,
,![]() ,满足
,满足![]() ;
;
③![]() ;
;
④若![]() ,则
,则![]() .
.
A.①②③B.①③④C.①②④D.②③④
查看答案和解析>>
科目: 来源: 题型:
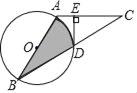
【题目】如图,AB是⊙O的直径,C是⊙O外一点,AB=AC,连接BC,交⊙O于点D,过点D作DE⊥AC,垂足为E.
(1)求证:DE与⊙O相切.
(2)若∠B=30°,AB=4,则图中阴影部分的面积是 (结果保留根号和π).
查看答案和解析>>
科目: 来源: 题型:
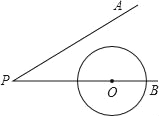
【题目】如图,∠APB=30°,圆心在PB上的⊙O的半径为1cm,OP=3cm,若⊙O沿BP方向平移,当⊙O与PA相切时,圆心O平移的距离为_____cm.
查看答案和解析>>
科目: 来源: 题型:
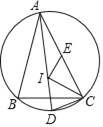
【题目】点I为△ABC的内心,连AI交△ABC的外接圆于点D,若AI=2CD,点E为弦AC的中点,连接EI,IC,若IC=6,ID=5,则IE的长为_____.
查看答案和解析>>
科目: 来源: 题型:
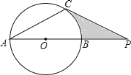
【题目】如图,已知:![]() 的直径
的直径![]() 与弦
与弦![]() 的夹角
的夹角![]() ,过点
,过点![]() 作
作![]() 的切线交
的切线交![]() 的延长线于点
的延长线于点![]() .
.
![]() 求证:
求证:![]() ;
;
![]() 的直径是
的直径是![]() ,以点
,以点![]() 为圆心作圆,当半径为多长时,
为圆心作圆,当半径为多长时,![]() 与
与![]() 相切?
相切?
![]() 若
若![]() ,求图中阴影部分的面积(结果精确到
,求图中阴影部分的面积(结果精确到![]() ,
,![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com