
科目: 来源: 题型:
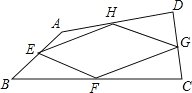
【题目】(满分8分)我们把依次连接任意四边形各边中点得到的四边形叫做中点四边形.
如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点,依次连接各边中点得到中点四边形EFGH.
(1)这个中点四边形EFGH的形状是____________;
(2)证明你的结论.
查看答案和解析>>
科目: 来源: 题型:
【题目】(本小题满分10分 )在端午节前夕三位同学到某超市调研一种进价为2元的粽子的售销情况,请跟据小丽提供的信息,解答小华和小明提出的问题
小丽:每个定价3元,每天能卖出500个,而且,这种粽子每上涨0.1元,其售销量将减小10个
小华:照你所说,如果实现每天800元的售销利润,那该如何定价?莫忘了物价局规定售价不能超过进价的240%哟
小明:800元售销利润是不是最多的呢?如果不是,那该如何定价,才会使每天的利润最大?.
(1)小华的问题解答:
(2)小明的问题解答:
查看答案和解析>>
科目: 来源: 题型:
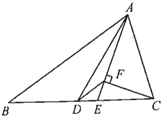
【题目】如图所示,在![]() 中,AB>AC,AD是中线,AE是角平分线,CF⊥AE于点F,连接DF,则①DF//AB;②∠DAE=
中,AB>AC,AD是中线,AE是角平分线,CF⊥AE于点F,连接DF,则①DF//AB;②∠DAE=![]() (∠ACB-∠ABC);③DF=
(∠ACB-∠ABC);③DF=![]() (AB-AC);④
(AB-AC);④![]() (AB-AC)<AD<
(AB-AC)<AD<![]() (AB+AC).其中正确的是__________.
(AB+AC).其中正确的是__________.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,点F在AC延长线上,![]() ,DE是△ABC中位线,如果∠1=30°,DE=2,则四边形AFED的周长是________
,DE是△ABC中位线,如果∠1=30°,DE=2,则四边形AFED的周长是________

查看答案和解析>>
科目: 来源: 题型:
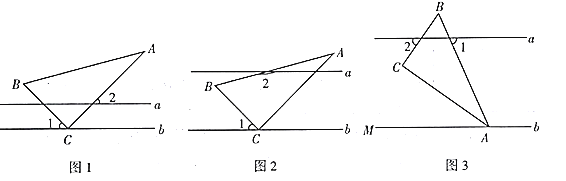
【题目】在综合与实践课上,同学们以“一个含![]() 的直角三角尺和两条平行线”为背景开展数学活动,如图,已知两直线
的直角三角尺和两条平行线”为背景开展数学活动,如图,已知两直线![]() 且
且![]() 和直角三角形
和直角三角形![]() ,
,![]() ,
,![]() ,
,![]() .
.
操作发现:
(1)在如图1中,![]() ,求
,求![]() 的度数;
的度数;
(2)如图2,创新小组的同学把直线![]() 向上平移,并把
向上平移,并把![]() 的位置改变,发现
的位置改变,发现![]() ,说明理由;
,说明理由;
实践探究:
(3)缜密小组在创新小组发现结论的基础上,将如图中的图形继续变化得到如图,![]() 平分
平分![]() ,此时发现
,此时发现![]() 与
与![]() 又存在新的数量关系,请直接写出
又存在新的数量关系,请直接写出![]() 与
与![]() 的数量关系.
的数量关系.
查看答案和解析>>
科目: 来源: 题型:
【题目】先阅读下列两段材料,再解答下列问题:
(一)例题:分解因式:![]()
解:将“![]() ”看成整体,设
”看成整体,设![]() ,则原式
,则原式![]() ,
,
再将“![]() ”换原,得原式
”换原,得原式![]() ;
;
上述解题目用到的是:整体思想,“整体思想”是数学解题中常用的一种思想方法;
(二)常用因式分解的方法有提公因式法和公式法,但有的多项式只用上述一种方法无法分解,例如![]() ,我们细心观察就会发现,前面两项可以分解,后两项也可以分解,分别分解后会产生公因式就可以完整分解了.
,我们细心观察就会发现,前面两项可以分解,后两项也可以分解,分别分解后会产生公因式就可以完整分解了.
过程:![]()
![]() ,
,
这种方法叫分组分解法,对于超过三项的多项式往往考虑这种方法.
利用上述数学思想方法解决下列问题:
(1)分解因式:![]()
(2)分解因式:![]()
(3)分解因式:![]() ;
;
查看答案和解析>>
科目: 来源: 题型:
【题目】已知二次函数![]() ,完成下列各题:
,完成下列各题:

![]() 将函数关系式用配方法化为
将函数关系式用配方法化为![]() 的形式,并写出它的顶点坐标、对称轴.
的形式,并写出它的顶点坐标、对称轴.
![]() 求出它的图象与坐标轴的交点坐标.
求出它的图象与坐标轴的交点坐标.
![]() 在直角坐标系中,画出它的图象.
在直角坐标系中,画出它的图象.
![]() 根据图象说明:当
根据图象说明:当![]() 为何值时,
为何值时,![]() ;当
;当![]() 为何值时,
为何值时,![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图①,已知抛物线y=ax2+bx+c的图像经过点A(0,3)、B(1,0),其对称轴为直线l:x=2,过点A作AC∥x轴交抛物线于点C,∠AOB的平分线交线段AC于点E,点P是抛物线上的一个动点,设其横坐标为m.
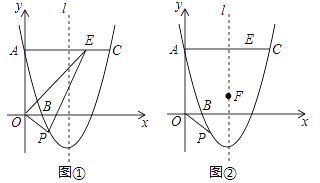
(1)求抛物线的解析式;
(2)若动点P在直线OE下方的抛物线上,连结PE、PO,当m为何值时,四边形AOPE面积最大,并求出其最大值;
(3)如图②,F是抛物线的对称轴l上的一点,在抛物线上是否存在点P使△POF成为以点P为直角顶点的等腰直角三角形?若存在,直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com