
科目: 来源: 题型:
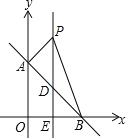
【题目】如图,平面直角坐标系中,直线AB:y=﹣x+b交y轴于点A(0,4),交x轴于点B.
(1)求直线AB的表达式和点B的坐标;
(2)直线l垂直平分OB交AB于点D,交x轴于点E,点P是直线l上一动点,且在点D的上方,设点P的纵坐标为n.
①用含n的代数式表示△ABP的面积;
②当S△ABP=8时,求点P的坐标;
③在②的条件下,以PB为斜边在第一象限作等腰直角△PBC,求点C的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】对于二次函数![]() ,有下列说法:
,有下列说法:
①如果当x≤1时![]() 随
随![]() 的增大而减小,则m≥1;
的增大而减小,则m≥1;
②如果它的图象与x轴的两交点的距离是4,则![]() ;
;
③如果将它的图象向左平移3个单位后的函数的最小值是-4,则m=-1;
④如果当x=1时的函数值与x=2013时的函数值相等,则当x=2014时的函数值为-3.
其中正确的说法是 .
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(﹣1,0),与y轴的交点B在(0,﹣2)和(0,﹣1)之间(不包括这两点),对称轴为直线x=1.下列结论:①abc>0 ②4a+2b+c>0 ③4ac﹣b2<8a ④![]() <a<
<a<![]() ⑤b>c.其中含所有正确结论的选项是( )
⑤b>c.其中含所有正确结论的选项是( )

A. ①③ B. ①③④ C. ②④⑤ D. ①③④⑤
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,抛物线m:y=ax2+b(a<0,b>0)与x轴于点A、B(点A在点B的左侧),与y轴交于点C.将抛物线m绕点B旋转180°,得到新的抛物线n,它的顶点为C1,与x轴的另一个交点为A1.若四边形AC1A1C为矩形,则a,b应满足的关系式为( )
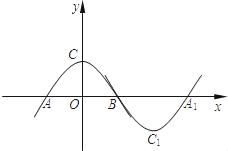
A. ab=﹣2 B. ab=﹣3 C. ab=﹣4 D. ab=﹣5
查看答案和解析>>
科目: 来源: 题型:
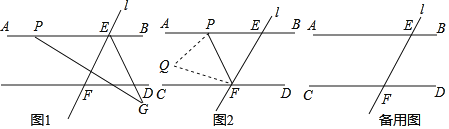
【题目】如图1,直线AB∥CD,直线l与直线AB,CD相交于点E,F,点P是射线EA上的一个动点(不包括端点)
(1)若∠CFE=119°,PG交∠FEB的平分线EG于点G,∠APG=150°,则∠G的大小为 .
(2)如图2,连接PF.将△EPF折叠,顶点E落在点Q处.
①若∠PEF=48°,点Q刚好落在其中的一条平行线上,请直接写出∠EFP的大小为 .
②若∠PEF=75°,∠CFQ=![]() ∠PFC,求∠EFP的度数.
∠PFC,求∠EFP的度数.
查看答案和解析>>
科目: 来源: 题型:
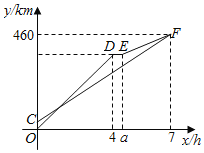
【题目】甲、乙两车从A地出发,沿同一路线驶向B地,甲车先出发匀速驶向B地,40min后,乙车出发,匀速行驶一段时间后,在途中的货站装货耗时半小时.由于满载货物,为了行驶安全,速度减少了50km/h,结果与甲车同时到达B地,甲乙两车距A地的路程y(km)与乙车行驶时间x(h)之间的函数图象如图所示
(1)a= ,甲的速度是 km/h;
(2)求线段CF对应的函数表达式,并求乙刚到达货站时,甲距B地还有多远?
(3)乙车出发 min追上甲车?
(4)直接写出甲出发多长时间,甲乙两车相距40km.
查看答案和解析>>
科目: 来源: 题型:
【题目】某城市为创建国家卫生城市,需要购买甲、乙两种类型的分类垃圾桶(如图所示),据调查该城市的A、B、C三个社区积极响应号并购买,具体购买的数和总价如表所示.
社区 | 甲型垃圾桶 | 乙型垃圾桶 | 总价 |
A | 10 | 8 | 3320 |
B | 5 | 9 | 2860 |
C | a | b | 2820 |
(1)运用本学期所学知识,列二元一次方程组求甲型垃圾桶、乙型垃圾桶的单价每套分别是多少元?
(2)按要求各个社区两种类型的垃圾桶都要有,则a= .

查看答案和解析>>
科目: 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(﹣1,0),对称轴为直线x=2,下列结论:(1)4a+b=0;(2)9a+c>3b;(3)8a+7b+2c>0;(4)若点A(﹣3,y1)、点B(﹣![]() ,y2)、点C(
,y2)、点C(![]() ,y3)在该函数图象上,则y1<y3<y2;(5)若方程a(x+1)(x﹣5)=﹣3的两根为x1和x2,且x1<x2,则x1<﹣1<5<x2.其中正确的结论有( )
,y3)在该函数图象上,则y1<y3<y2;(5)若方程a(x+1)(x﹣5)=﹣3的两根为x1和x2,且x1<x2,则x1<﹣1<5<x2.其中正确的结论有( )
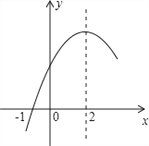
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com