科目： 来源： 题型：
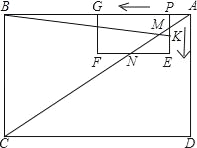
【题目】如图，在矩形ABCD和矩形PEFG中，AB=8，BC=6，PE=2，PG=4．PE与AC交于点M，EF与AC交于点N，动点P从点A出发沿AB以每秒1个单位长的速度向点B匀速运动，伴随点P的运动，矩形PEFG在射线AB上滑动；动点K从点P出发沿折线PE﹣﹣EF以每秒1个单位长的速度匀速运动．点P、K同时开始运动，当点K到达点F时停止运动，点P也随之停止．设点P、K运动的时间是t秒（t＞0）．
（1）当t=1时，KE=_____，EN=_____；
（2）当t为何值时，△APM的面积与△MNE的面积相等？
（3）当点K到达点N时，求出t的值；
（4）当t为何值时，△PKB是直角三角形？
查看答案和解析>>
科目： 来源： 题型：
【题目】在△ABC中，∠ACB=90°，BE是AC边上的中线，点D在射线BC上．
发现：如图1，点D在BC边上，CD：BD=1：2，AD与BE相交于点P，过点A作AF∥BC，交BE的延长线于点F，求
的值为．
解决问题：如图2，在△ABC中，∠ACB=90°，点D在BC的延长线上，AD与AC边上的中线BE的延长线交于点P，DC：BC=1：2．求的值.
应用：若CD=2，AC=6，求BP的值．
查看答案和解析>>
科目： 来源： 题型：
【题目】某日王老师佩戴运动手环进行快走锻炼，两次锻炼后数据如表．与第一次锻炼相比，王老师第二次锻炼步数增长的百分率是其平均步长减少的百分率的3倍．设王老师第二次锻炼时平均步长减少的百分率为
．
项目 | 第一次锻炼 | 第二次锻炼 |
步数(步) | 10000 | ____________ |
平均步长(米/步) | 0.6 | ____________ |
距离(米) | 6000 | 7020 |
注：步数×平均步长＝距离．
(1)根据题意完成表格填空；
(2)求x；
(3)王老师发现好友中步数排名第一为24000步，因此在两次锻炼结束后又走了500米，使得总步数恰好为24000步，求王老师这500米的平均步长．
查看答案和解析>>
科目： 来源： 题型：
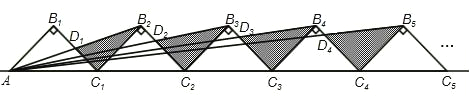
【题目】如图所示，n+1个直角边长为1的等腰直角三角形，斜边在同一直线上，设△B2D1C1的面积为S1，△B3D2C2的面积为S2，…，△Bn+1DnCn的面积为Sn，则S1= ，Sn= （用含n的式子表示）．
查看答案和解析>>
科目： 来源： 题型：
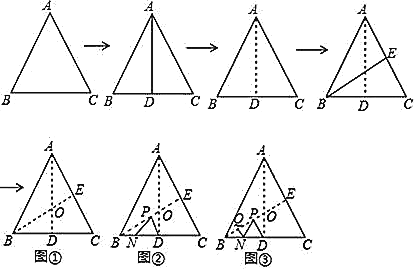
【题目】如图，将边长为6的正三角形纸片ABC按如下顺序进行两次折叠，展开后，得折痕AD、BE．(如图①)，点O为其交点．如图②，若P、N分别为BE、BC上的动点．如图③，若点Q在线段BO上，BQ=1，则QN+NP+PD的最小值=_______．
查看答案和解析>>
科目： 来源： 题型：
【题目】问题背景：（1）如图
，已知
中，
，直线
经过点
直线，
直线，垂足分别为点
．求证：
．
证明：
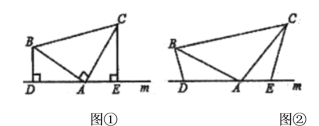
拓展延伸：（2）如图
，将（1）中的条件改为：在中，
三点都在直线上，并且有
．请写出
三条线段的数量关系．（不需要证明）
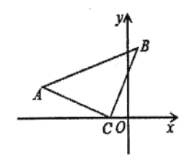
实际应用：（3）如图，在
中，
，点
的坐标为
，点
的坐标为
，请直接写出点
的坐标．
查看答案和解析>>
科目： 来源： 题型：
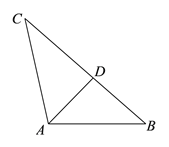
【题目】从三角形一个顶点引出一条射线于对边相交，顶点与交点之间的线段把这个三角形分割成两个小三角形，如果分得的两个小三角形中一个为等腰三角形，另一个与原三角形相似，我们把这条线段叫做这个三角形的优美线．
（1）如图，在△ABC中，AD为角平分线，∠B=50°，∠C=30°，求证：AD为△ABC的优美线；
（2）在△ABC中，∠B=46°，AD是△ABC的优美线，且△ABD是以AB为腰的等腰三角形，求∠BAC的度数；
（3）在△ABC中，AB=4，AC=2，AD是△ABC的优美线，且△ABD是等腰三角形，直接写出优美线AD的长．
查看答案和解析>>
科目： 来源： 题型：
【题目】在社会主义新农村建设中，某乡镇决定对一段公路进行改造，已知这项工程由甲工程队单独做需要40天完成；如果由乙工程先单独做10天，那么剩下的工程还需要两队合做20天才能完成．
（1）求乙工程队单独完成这项工程所需的天数；
（2）求两队合作完成这项工程所需的天数．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com