
科目: 来源: 题型:
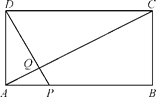
【题目】如图,矩形ABCD中,AB=20,BC=10,点P为AB边上一动点,DP交AC于点Q.
(1)求证:△APQ∽△CDQ;
(2)P点从A点出发沿AB边以每秒1个单位长度的速度向B点移动,移动时间为t秒.当t为何值时,DP⊥AC?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,A,B,C三点在同一直线上,分别以AB,BC(AB>BC)为边,在直线AC的同侧作等边ΔABD和等边ΔBCE,连接AE交BD于点M,连接CD交BE于点N,连接MN. 以下结论:①AE=DC,②MN//AB,③BD⊥AE,④∠DPM=60°,⑤ΔBMN是等边三角形.其中正确的是__________(把所有正确的序号都填上).

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠A=36°,AB的垂直平分线DE交AC于D,交AB于E,下述结论:①BD平分∠ABC;②AD=BD=BC;③△BDC的周长等于AB+BC;④D是AC中点.其中正确的命题序号是( )
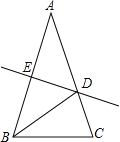
A.①②③ B.①②④ C.②③④ D.①③④
查看答案和解析>>
科目: 来源: 题型:
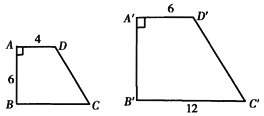
【题目】已知:如图,梯形ABCD与梯形A′B′C′D′相似,AD∥BC,A′D′∥B′C′,∠A=∠A′.AD=4,A′D′=6,AB=6,B′C′=12.求:
(1)梯形ABCD与梯形A′B′C′D′的相似比k;
(2)A′B′和BC的长;
(3)D′C′∶DC.
查看答案和解析>>
科目: 来源: 题型:
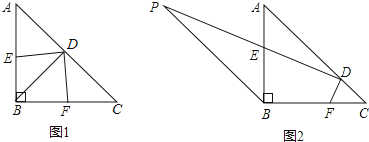
【题目】在等腰三角形ABC中,∠ABC=90度,D是AC边上的动点,连结BD,E、F分别是AB、BC上的点,且DE⊥DF.、(1)如图1,若D为AC边上的中点.
(1)填空:∠C= ,∠DBC= ;
(2)求证:△BDE≌△CDF.
(3)如图2,D从点C出发,点E在PD上,以每秒1个单位的速度向终点A运动,过点B作BP∥AC,且PB=AC=4,点E在PD上,设点D运动的时间为t秒(0≤1≤4)在点D运动的过程中,图中能否出现全等三角形?若能,请直接写出t的值以及所对应的全等三角形的对数,若不能,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,∠ACB=45°,过点A作AD⊥BC于点D,点E为AD上一点,且ED=BD.
(1)求证:△ABD≌△CED;
(2)若CE为∠ACD的角平分线,求∠BAC的度数.

查看答案和解析>>
科目: 来源: 题型:
【题目】列分式方程解应用题.
为缓解市区至通州沿线的通勤压力,北京市政府利用既有国铁线路富余能力,通过线路及站台改造,开通了“京通号”城际动车组,每班动车组预定运送乘客1200人,为提高运输效率,“京通号”车组对动车车厢进行了改装,使得每节车厢乘坐的人数比改装前多了![]() ,运送预定数量的乘客所需要的车厢数比改装前减少了4节,求改装后每节车厢可以搭载的乘客人数.
,运送预定数量的乘客所需要的车厢数比改装前减少了4节,求改装后每节车厢可以搭载的乘客人数.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在ABCD中,AC,BD相交于点O,点E是OA的中点,连接BE并延长交AD于点F,已知S△AEF=4,则下列结论:①![]() ;②S△BCE=36;③S△ABE=12;④△AEF~△ACD,其中一定正确的是( )
;②S△BCE=36;③S△ABE=12;④△AEF~△ACD,其中一定正确的是( )
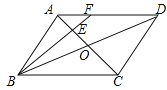
A. ①②③④ B. ①④ C. ②③④ D. ①②③
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:如图,△ABC中,P、Q两点分别是边AB和AC的垂直平分线与BC的交点,连结AP和AQ,且BP=PQ=QC.求∠C的度数.
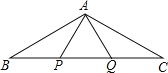
证明:∵P、Q两点分别是边AB和AC的垂直平分线与BC的交点,
∴PA= ,QC=QA.
∵BP=PQ=QC,
∴在△APQ中,PQ= (等量代换)
∴△APQ是 三角形.
∴∠AQP=60°,
∵在△AQC中,QC=QA,
∴∠C=∠ .
又∵∠AQP是△AQC的外角,
∴∠AQP=∠ +∠ =60°.(三角形的一个外角等于与它不相邻的两个内角的和)
∴∠C= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com