
科目: 来源: 题型:
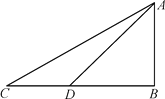
【题目】如图,某校数学兴趣小组为测得校园里旗杆AB的高度,在操场的平地上选择一点C,测得旗杆顶端A的仰角为30,再向旗杆的方向前进16米,到达点D处(C,D,B三点在同一直线上),又测得旗杆顶端A的仰角为45,请计算旗杆AB的高度(结果保留根号).
查看答案和解析>>
科目: 来源: 题型:
【题目】贵阳市某消防支队在一幢居民楼前进行消防演习,如图所示,消防官兵利用云梯成功救出在C处的求救者后,发现在C处正上方17米的B处又有一名求救者,消防官兵立刻升高云梯将其救出,已知点A与居民楼的水平距离是15米,且在A点测得第一次施救时云梯与水平线的夹角∠CAD=60°,求第二次施救时云梯与水平线的夹角∠BAD的度数(结果精确到1°).

查看答案和解析>>
科目: 来源: 题型:
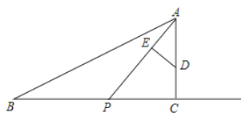
【题目】如图,已知在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 上的一点,
上的一点,![]() ,点
,点![]() 从
从![]() 点出发沿射线
点出发沿射线![]() 方向以每秒
方向以每秒![]() 个单位的速度向右运动.设点
个单位的速度向右运动.设点![]() 的运动时间为
的运动时间为![]() .连结
.连结![]() .
.
(1)当![]() 秒时,求
秒时,求![]() 的长度(结果保留根号);
的长度(结果保留根号);
(2)当![]() 为等腰三角形时,求
为等腰三角形时,求![]() 的值;
的值;
(3)过点![]() 做
做![]() 于点
于点![]() .在点
.在点![]() 的运动过程中,当
的运动过程中,当![]() 为何值时,能使
为何值时,能使![]() ?
?
查看答案和解析>>
科目: 来源: 题型:
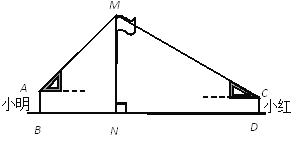
【题目】如图,在活动课上,小明和小红合作用一副三角板来测量学校旗杆高度.已知小明的眼睛与地面的距离(AB)是1.7m,他调整自己的位置,设法使得三角板的一条直角边保持水平,且斜边与旗杆顶端M在同一条直线上,测得旗杆顶端M仰角为45°;小红的眼睛与地面的距离(CD)是1.5m,用同样的方法测得旗杆顶端M的仰角为30°.两人相距28米且位于旗杆两侧(点B、N、D在同一条直线上).求出旗杆MN的高度.(参考数据: ![]() ,结果保留整数.)
,结果保留整数.)
查看答案和解析>>
科目: 来源: 题型:
【题目】某县为落实“精准扶贫惠民政策”,计划将某村的居民自来水管道进行改造.该工程若由甲队单独施工恰好在规定时间内完成;若乙队单独施工,则完成工程所需天数是规定天数的1.5倍.如果由甲、乙队先合作施工15天,那么余下的工程由甲队单独完成还需5天.
(1)这项工程的规定时间是多少天?
(2)为了缩短工期以减少对居民用水的影响,工程指挥部最终决定该工程由甲、乙两队合作完成.则甲、乙两队合作完成该工程需要多少天?
查看答案和解析>>
科目: 来源: 题型:
【题目】(2017重庆A卷第11题)如图,小王在长江边某瞭望台D处,测得江面上的渔船A的俯角为40°,若DE=3米,CE=2米,CE平行于江面AB,迎水坡BC的坡度i=1:0.75,坡长BC=10米,则此时AB的长约为( )(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84).

A. 5.1米 B. 6.3米 C. 7.1米 D. 9.2米
查看答案和解析>>
科目: 来源: 题型:
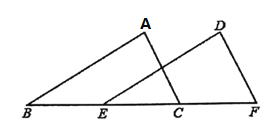
【题目】如图,在![]() 和
和![]() 中,
中,![]() 、
、![]() 、
、![]() 、
、![]() 在同一直线上,下面有四个条件,请你从中选三个作为题设,余下的一个作为结论,写出一个正确的命题,并加以证明.
在同一直线上,下面有四个条件,请你从中选三个作为题设,余下的一个作为结论,写出一个正确的命题,并加以证明.
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]()
解:我写的真命题是:
在![]() 和
和![]() 中,已知:___________________.
中,已知:___________________.
求证:_______________.(不能只填序号)
证明如下:
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,直线![]() ,直线
,直线![]() 分别与
分别与![]() ,
,![]() 相交于点
相交于点![]() 、
、![]() ,小宇同学利用尺规按以下步骤作图:①以点
,小宇同学利用尺规按以下步骤作图:①以点![]() 为圆心,以任意长为半径作弧交
为圆心,以任意长为半径作弧交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ②分别以
②分别以![]() ,
,![]() 为圆心,以大于,
为圆心,以大于,![]() 长为半径作弧,两弧在
长为半径作弧,两弧在![]() 内交于点
内交于点![]() ;③作射线
;③作射线![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,则
,则![]() ____________.
____________.

查看答案和解析>>
科目: 来源: 题型:
【题目】点P的“d值”定义如下:若点Q为圆上任意一点,线段PQ长度的最大值与最小值之差即为点P的“d值”,记为dP.特别的,当点P,Q重合时,线段PQ的长度为0.当⊙O的半径为2时:
(1)若点C(﹣![]() ,0),D(3,4),则dc= ,dp= ;
,0),D(3,4),则dc= ,dp= ;
(2)若在直线y=2x+2上存在点P,使得dP=2,求出点P的横坐标;
(3)直线y=﹣![]() x+b(b>0)与x轴,y轴分别交于点A,B.若线段AB上存在点P,使得2≤dP<3,请你直接写出b的取值范围.
x+b(b>0)与x轴,y轴分别交于点A,B.若线段AB上存在点P,使得2≤dP<3,请你直接写出b的取值范围.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com