
科目: 来源: 题型:
【题目】某县为了落实中央的“强基惠民工程”,计划将某村的居民自来水管道进行改造.该工程若由甲队单独施工恰好在规定时间内完成;若乙队单独施工,则完成工程所需天数是规定天数的1.5倍.如果由甲、乙队先合做15天,那么余下的工程由甲队单独完成还需5天.
(1)这项工程的规定时间是多少天?
(2)已知甲队每天的施工费用为6500元,乙队每天的施工费用为3500元.为了缩短工期以减少对居民用水的影响,工程指挥部最终决定该工程由甲、乙队合做来完成.则该工程施工费用是多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】科幻小说《实验室的故事》中,有这样一个情节,科学家把一种珍奇的植物分别放在不同温度的环境中,经过一段时间后,记录下这种植物高度的增长情况(如下表):
温度x/℃ | … | ﹣4 | ﹣2 | 0 | 2 | 4 | 6 | … |
植物每天高度的增长量y/mm | … | 41 | 49 | 49 | 41 | 25 | 1 | … |
由这些数据,科学家推测出植物每天高度的增长量y是温度x的二次函数,那么下列三个结论:
①该植物在0℃时,每天高度的增长量最大;
②该植物在﹣6℃时,每天高度的增长量能保持在25mm左右;
③该植物与大多数植物不同,6℃以上的环境下高度几乎不增长.
上述结论中,所有正确结论的序号是
A. ①②③ B. ①③ C. ①② D. ②③
查看答案和解析>>
科目: 来源: 题型:
【题目】在边长为的小正方形组成的正方形网格中建立如图所示的平面直角坐标系,已知格点三角形![]() (三角形的三个顶点都在小正方形的顶点上)
(三角形的三个顶点都在小正方形的顶点上)
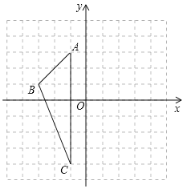
(1)写出![]() 的面积;
的面积;
(2)画出![]() 关于
关于![]() 轴对称的
轴对称的![]() ;
;
(3)写出点![]() 及其对称点
及其对称点![]() 的坐标.
的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,C、E和B、D、F分别在∠GAH的两边上,且AB=BC=CD=DE=EF,若∠A=18°,则∠GEF的度数是( )

A. 80° B. 90° C. 100° D. 108°
查看答案和解析>>
科目: 来源: 题型:
【题目】已知反比例函数y=﹣![]() ,下列结论:①图象必经过点(﹣3,1);②图象在第二,四象限内;③y随x的增大而增大;④当x>﹣1时,y>3.其中错误的结论有( )
,下列结论:①图象必经过点(﹣3,1);②图象在第二,四象限内;③y随x的增大而增大;④当x>﹣1时,y>3.其中错误的结论有( )
A. ①④ B. ②③ C. ②④ D. ③④
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,Rt△ACB中,∠ACB=90°,AC=BC,E点为射线CB上一动点,连结AE,作AF⊥AE且AF=AE.
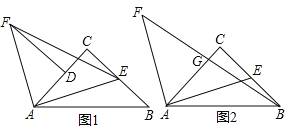
(1)如图1,过F点作FD⊥AC交AC于D点,求证:FD=BC;
(2)如图2,连结BF交AC于G点,若AG=3,CG=1,求证:E点为BC中点;
(3)当E点在射线CB上,连结BF与直线AC交于G点,若BC=4,BE=3,则![]() = (直接写出结果)
= (直接写出结果)
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读:如图1,在△ABC中,BE是AC边上的中线, D是BC边上的一点,CD:BD=1:2,AD与BE相交于点P,求![]() 的值.小昊发现,过点A作AF∥BC,交BE的延长线于点F,通过构造△AEF,经过推理和计算能够使问题得到解决(如图2).
的值.小昊发现,过点A作AF∥BC,交BE的延长线于点F,通过构造△AEF,经过推理和计算能够使问题得到解决(如图2).

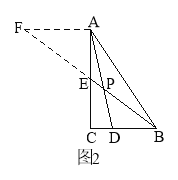
(1)![]() 的值为 ;
的值为 ;
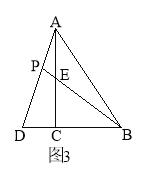
(2)参考小昊思考问题的方法,解决问题:
如图3,在△ABC中,∠ACB=90°,点D在BC的延长线上,AD与AC边上的中线BE的延长线交于点P,DC:BC:AC=1:2:3 .
![]() 求
求![]() 的值;
的值;
![]() 若CD=2,求BP的长.
若CD=2,求BP的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,AB是⊙O的直径,C是弧![]() 的中点,⊙O的切线BD交AC的延长线于点D,E是OB的中点,CE的延长线交切线BD于点F,AF交⊙O于点H,连接BH.
的中点,⊙O的切线BD交AC的延长线于点D,E是OB的中点,CE的延长线交切线BD于点F,AF交⊙O于点H,连接BH.
⑴求证:AC=CD.
⑵若OB=2,求BH的长.

查看答案和解析>>
科目: 来源: 题型:
【题目】定义:如图①,点M、N把线段AB分割成AM、MN和BN,若以AM,MN、BN为边的三角形是一个直角三角形,则称点M,N是线段AB的勾股分割点.

(1)已知点M、N是线段AB的勾股分割点,若AM=2,MN=3,求BN的长;
(2)如图2,在Rt△ABC中,AC=BC,点M,N在斜边AB上,∠MCN=45°,求证:点M,N是线段AB的勾股分割点(提示:把△ACM绕点C逆时针旋转90°)
(3)在(2)的前提下,若∠BCN=15°,BN=1.求AN的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】杭州某游乐园门票价格为每人100元,20人以上(含20人)的团体票8折优惠.
(1)建兰中学初二年级一等奖学金获得者共有18人,学校奖励他们去游玩,你认为学校买18张门票,还是多买2张(买20张)购团体票更合算?
(2)如果获奖的学生不足20人,那么人数达到多少人时购买团体票比买普通票更合算.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com