
科目: 来源: 题型:
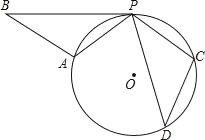
【题目】如图,已知△PDC是⊙O的内接三角形,CP=CD,若将△PCD绕点P顺时针旋转,当点C刚落在⊙O上的A处时,停止旋转,此时点D落在点B处.
(1)求证:PB与⊙O相切;
(2)当PD=2![]() ,∠DPC=30°时,求⊙O的半径长.
,∠DPC=30°时,求⊙O的半径长.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,AB是⊙O的直径,D为⊙O上一点,OD⊥AC,垂足为E,连接BD.

(1)求证:BD平分∠ABC;
(2) 当∠ODB=30°时,求证:BC=OD.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知有两辆玩具车进行30米的直跑道比赛,两车从起点同时出发,A车到达终点时,B车离终点还差12米,A车的平均速度为2.5米/秒.
(1)求B车的平均速度;
(2)如果两车重新比赛,A车从起点退后12米,两车能否同时到达终点?请说明理由;
(3)在(2)的条件下,若调整A车的平均速度,使两车恰好同时到达终点,求调整后A车的平均速度.
查看答案和解析>>
科目: 来源: 题型:
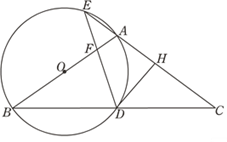
【题目】如图,在△ABC中,AB=AC,以AB为直径作圆O,分别交BC于点D,交CA的延长线于点E,过点D作DH⊥AC于点H,连接DE交线段OA于点F.
(1)求证:DH是圆O的切线;
(2)若![]() ,求证:A为EH的中点.
,求证:A为EH的中点.
(3)若EA=EF=1,求圆O的半径.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:如图,AB是⊙O的直径,点P在BA的延长线上,弦CD交AB于E,连接OD、PC、BC,∠AOD=2∠ABC,∠P=∠D,过E作弦GF⊥BC交圆与G、F两点,连接CF、BG.则下列结论:①CD⊥AB;②PC是⊙O的切线;③OD∥GF;④弦CF的弦心距等于![]() BG.则其中正确的是( )
BG.则其中正确的是( )

A. ①②④ B. ③④ C. ①②③ D. ①②③④
查看答案和解析>>
科目: 来源: 题型:
【题目】问题发现:
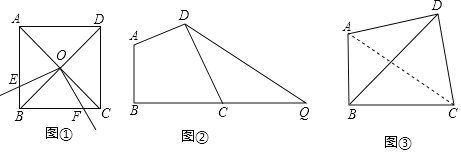
(1)如图①,正方形ABCD的边长为4,对角线AC、BD相交于点O,E是AB上点(点E不与A、B重合),将射线OE绕点O逆时针旋转90°,所得射线与BC交于点F,则四边形OEBF的面积为 .
问题探究:
(2)如图②,线段BQ=10,C为BQ上点,在BQ上方作四边形ABCD,使∠ABC=∠ADC=90°,且AD=CD,连接DQ,求DQ的最小值;
问题解决:
(3)“绿水青山就是金山银山”,某市在生态治理活动中新建了一处南山植物园,图③为南山植物园花卉展示区的部分平面示意图,在四边形ABCD中,∠ABC=∠ADC=90°,AD=CD,AC=600米.其中AB、BD、BC为观赏小路,设计人员考虑到为分散人流和便观赏,提出三条小路的长度和要取得最大,试求AB+BD+BC的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】为迎接购物节,某网店准备购进甲、乙两种运动鞋,甲种运动鞋每双的进价比乙种运动鞋每双的进价多60元,用30000元购进甲种运动鞋的数量与用21000元购进乙种运动鞋的数量相同.
(1)求甲、乙两种运动鞋的进价(用列分式方程的方法解答):
(2)该网店老板计划购进这两种运动鞋共200双,且甲种运动鞋的进货数量不少于乙种运动鞋数量的![]() ,甲种运动鞋每双售价为350元,乙种运动鞋每双售价为300元.设甲种运动鞋的进货量为m双,销售完甲、乙两种运动鞋的总利润为w元,求w与m的函数关系式,并求总利润的最大值.
,甲种运动鞋每双售价为350元,乙种运动鞋每双售价为300元.设甲种运动鞋的进货量为m双,销售完甲、乙两种运动鞋的总利润为w元,求w与m的函数关系式,并求总利润的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,△ABC内接于⊙O,OD⊥BC于D,∠OCD=40°,则弦BC所对圆周角的度数是( )
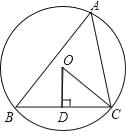
A. 40° B. 50° C. 50°或130° D. 40°或140°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com