
科目: 来源: 题型:
【题目】某商店销售一种商品,通过记录,发现该商品从开始销售至销售的第x天结束时(x为整数)的总销量y(件)满足二次函数关系,销量情况记录如下表:
x | 0 | 1 | 2 | 3 |
y | 0 | 58 | 112 | 162 |
(1)求y与x之间的函数关系式(不需要写自变量的取值范围);
(2)求:销售到第几天结束时,该商品全部售完?
(3)若第m天的销量为22件,求m的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知![]() 是等边三角形,点
是等边三角形,点![]() 是直线
是直线![]() 上一点,以
上一点,以![]() 为一边在
为一边在![]() 的右侧作等边
的右侧作等边![]() .
.
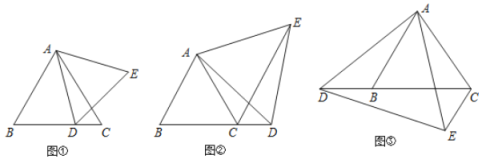
(1)如图①,点![]() 在线段
在线段![]() 上移动时,直接写出
上移动时,直接写出![]() 和
和![]() 的大小关系;
的大小关系;
(2)如图②,点![]() 在线段
在线段![]() 的延长线上移动时,猜想
的延长线上移动时,猜想![]() 的大小是否发生变化.若不变请求出其大小;若变化,请说明理由.
的大小是否发生变化.若不变请求出其大小;若变化,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】为“厉行节能减排,倡导绿色出行”,某公司拟在我县甲、乙两个街道社区试点投放一批共享单车(俗称“小黄车”),这批自行车包括A、B两种不同款型,投放情况如下表:
成本单价 (单位:元) | 投放数量(单位:辆) | 总价(单位:元) | |
A型 |
| 50 | 50 |
B型 |
| 50 |
|
成本合计(单位:元) | 7500 | ||
(1)根据表格填空:
本次试点投放的A、B型“小黄车”共有 辆;用含有![]() 的式子表示出B型自行车的成本总价为 ;
的式子表示出B型自行车的成本总价为 ;
(2)试求A、B两种款型自行车的单价各是多少元?
(3)经过试点投放调查,现在该公司决定采取如下方式投放A型“小黄车”:甲街区每100人投放n辆,乙街区每100人投放(n+2)辆,按照这种投放方式,甲街区共投放1500辆,乙街区共投放1200辆,如果两个街区共有![]() 人,求甲街区每100人投放A型“小黄车”的数量.
人,求甲街区每100人投放A型“小黄车”的数量.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:关于x的方程:mx2﹣(3m﹣1)x+2m﹣2=0.
(1)求证:无论m取何值时,方程恒有实数根;
(2)若关于x的二次函数y=mx2﹣(3m﹣1)x+2m﹣2的图象与x轴两交点间的距离为2时,求抛物线的解析式.
查看答案和解析>>
科目: 来源: 题型:
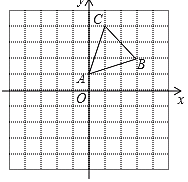
【题目】如图,在平面直角坐标系中,△ABC的顶点A(0,1),B(3,2),C(1,4)均在正方形网格的格点上.
(1)画出△ABC关于x轴的对称图形△A1B1C1;
(2)将△A1B1C1沿x轴方向向左平移4个单位得到△A2B2C2,画出△A2B2C2并写出顶点A2,B2,C2的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】(6分)如图,在建立了平面直角坐标系的正方形网格中,A(2,2),B(1,0),C(3,1)

(1)画出ΔABC关于x轴对称的ΔA1B1C1.
(2)画出将ΔABC绕点B逆时针旋转900,所得的ΔA2B2C2.
(3)直接写出A2点的坐标.
查看答案和解析>>
科目: 来源: 题型:
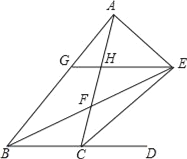
【题目】如图,△ABC的内角∠ABC和外角∠ACD的平分线相交于点E,BE交AC于点F,过点E作EG∥BD交AB于点G,交AC于点H,连接AE,有以下结论:
①∠BEC=![]() ∠BAC;②△HEF≌△CBF;③BG=CH+GH;④∠AEB+∠ACE=90°,其中正确的结论有_____(将所有正确答案的序号填写在横线上).
∠BAC;②△HEF≌△CBF;③BG=CH+GH;④∠AEB+∠ACE=90°,其中正确的结论有_____(将所有正确答案的序号填写在横线上).
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,以△ABC的一边为边画等腰三角形,使得它的第三个顶点在△ABC的其他边上,则可以画出的不同的等腰三角形的个数最多为( )

A. 4 B. 5 C. 6 D. 7
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,B、C、D在同一直线上,△ABC和△ECD都是等边三角形,BE与AD相交于点M,
(1)求证:∠CBE=∠CAD;
(2)由(1)可知,图中的△EBC是由△DAC怎样变换(填一种变换)得到的.

查看答案和解析>>
科目: 来源: 题型:
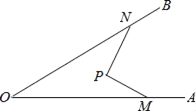
【题目】如图,∠AOB=30°,P点在∠AOB内部,M点在射线OA上,将线段PM绕P点逆时针旋转90°,M点恰好落在OB上的N点(OM>ON),若PM=![]() ,ON=8,则OM=_____.
,ON=8,则OM=_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com