
科目: 来源: 题型:
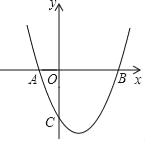
【题目】如图,已知抛物线y=ax2+bx﹣3过点A(﹣1,0),B(3,0),点M、N为抛物线上的动点,过点M作MD∥y轴,交直线BC于点D,交x轴于点E.过点N作NF⊥x轴,垂足为点F
(1)求二次函数y=ax2+bx﹣3的表达式;
(2)若M点是抛物线上对称轴右侧的点,且四边形MNFE为正方形,求该正方形的面积;
(3)若M点是抛物线上对称轴左侧的点,且∠DMN=90°,MD=MN,请直接写出点M的横坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,△ABC是边长为8的等边三角形,AD⊥BC下点D,DE⊥AB于点E
(1)求证:AE=3EB;
(2)若点F是AD的中点,点P是BC边上的动点,连接PE,PF,如图2所示,求PE+PF的最小值及此时BP的长;
(3)在(2)的条件下,连接EF,若AD=![]() ,当PE+PF取最小值时,△PEF的面积是 .
,当PE+PF取最小值时,△PEF的面积是 .

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,AD是△ABC的角平分线,线段AD的垂直平分线分别交AB和AC于点E、F,连接DE、DF.
(1)试判定四边形AEDF的形状,并证明你的结论.
(2)若AE=5,AD=8,求EF的长.
(3)△ABC满足什么条件时,四边形AEDF是正方形?

查看答案和解析>>
科目: 来源: 题型:
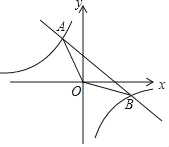
【题目】如图,O为坐标原点,点A(﹣1,5)和点B(m,﹣1)均在反比例函数![]() 图象上
图象上
(1)求m,k的值;
(2)当x满足什么条件时,﹣x+4>﹣![]() ;
;
(3)P为y轴上一点,若△ABP的面积是△ABO面积的2倍,直接写出点P的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】我们都知道连接多边形任意不相邻的两点的线段成为多边形的对角线,也都知道四边形的对角线有2条,五边形的对角线有5条
(1)六边形的对角线有 条,七边形的对角线有 条;
(2)多边形的对角线可以共有20条吗?如果可以,求出多边形的边数,如果不可以,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】经过某路口的行人,可能直行,也可能左拐或右拐.假设这三种可能性相同,现有两人经过该路口,求下列事件的概率:
(1)“两人都左拐”的概率是 ;恰好有一人直行,另一人左拐的概率是 ;
(2)利用列表法或树状图求出“至少有一人直行”的概率.
查看答案和解析>>
科目: 来源: 题型:
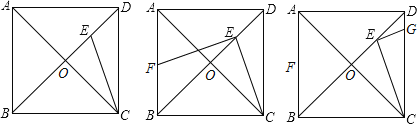
【题目】如图,已知正方形ABCD的边长为![]() ,连接AC、BD交于点O,CE平分∠ACD交BD于点E,
,连接AC、BD交于点O,CE平分∠ACD交BD于点E,
(1)求DE的长;
(2)过点EF作EF⊥CE,交AB于点F,求BF的长;
(3)过点E作EG⊥CE,交CD于点G,求DG的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】某超市销售一种商品,成本每千克40元,规定每千克售价不低于成本,且不高于80元,经市场调查,每天的销售量y(千克)与每千克售价x(元)满足一次函数关系,部分数据如下表:
售价x(元/千克) | 50 | 60 | 70 |
销售量y(千克) | 100 | 80 | 60 |
(1)求y与x之间的函数表达式;
(2)设商品每天的总利润为W(元),求W与x之间的函数表达式(利润=收入﹣成本),并指出售价为多少元时获得最大利润,最大利润是多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,我们把依次连接任意四边形ABCD各边中点所得四边形EFGH叫中点四边形.若四边形ABCD的面积记为S1,中点四边形EFGH的面积记为S2,则S1与S2的数量关系是( )
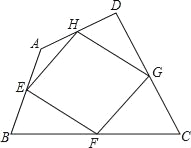
A. S1=3S2 B. 2S1=3S2 C. S1=2S2 D. 3S1=4S2
查看答案和解析>>
科目: 来源: 题型:
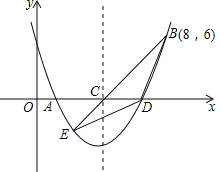
【题目】如图,二次函数y=![]() x2+bx+c的图象交x轴于A、D两点,并经过B点,已知A点坐标是(2,0),B点的坐标是(8,6).
x2+bx+c的图象交x轴于A、D两点,并经过B点,已知A点坐标是(2,0),B点的坐标是(8,6).
(1)求二次函数的解析式.
(2)求函数图象的顶点坐标及D点的坐标.
(3)该二次函数的对称轴交x轴于C点.连接BC,并延长BC交抛物线于E点,连接BD,DE,求△BDE的面积.
(4)抛物线上有一个动点P,与A,D两点构成△ADP,是否存在S△ADP=![]() S△BCD?若存在,请求出P点的坐标;若不存在.请说明理由.
S△BCD?若存在,请求出P点的坐标;若不存在.请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com