
科目: 来源: 题型:
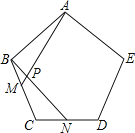
【题目】如图,点M、N分别是正五边形ABCDE的边BC、CD上的点,且BM=CN,AM交BN于点P.
(1)求证:△ABM≌△BCN;
(2)求∠APN的度数.
查看答案和解析>>
科目: 来源: 题型:
【题目】(6分)在一个不透明的纸箱里装有红、黄、蓝三种颜色的小球,它们除颜色外完全相同,其中红球有2个,黄球有1个,蓝球有1个.现有一张电影票,小明和小亮决定通过摸球游戏定输赢(赢的一方得电影票).游戏规则是:两人各摸1次球,先由小明从纸箱里随机摸出1个球,记录颜色后放回,将小球摇匀,再由小亮随机摸出1个球并记录颜色.若两人摸到的球颜色相同,则小明赢,否则小亮赢.这个游戏规则对双方公平吗?请你利用树状图或列表法说明理由
查看答案和解析>>
科目: 来源: 题型:
【题目】一只不透明的袋子中装有2个白球和1个红球,这些球除颜色外都相同,搅匀后从中任意摸出1个球(不放回),再从余下的2个球中任意摸出1个球.
(1)用树状图或列表等方法列出所有可能出现的结果;
(2)求两次摸到的球的颜色不同的概率.
查看答案和解析>>
科目: 来源: 题型:
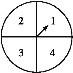
【题目】某超市计划在“十周年”庆典当天开展购物抽奖活动,凡当天在该超市购物的顾客,均有一次抽奖的机会,抽奖规则如下:如图,将圆形转盘平均分成四个扇形,分别标上1,2,3,4四个数字,抽奖者连续转动转盘两次,当每次转盘停止后指针所指扇形内的数字为每次所得的数(若指针指在分界线时重转);当两次所得数字之和为8时,返现金20元;当两次所得数字之和为7时,返现金15元;当两次所得数字之和为6时,返现金10元.某顾客参加一次抽奖,能获得返还现金的概率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
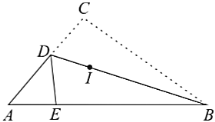
【题目】如图,三角形纸片![]() 中,沿过
中,沿过![]() 点的直线折叠这个三角形,使点
点的直线折叠这个三角形,使点![]() 落在
落在![]() 边上的点
边上的点![]() 处,折痕为
处,折痕为![]() ,则下列结论:
,则下列结论:
①![]() 平分
平分![]() ;
;
②![]() ;
;
③若![]() ,
,![]() ,
,![]() ,则
,则![]() 的周长为7;
的周长为7;
④![]() ;
;
⑤若![]() 平分
平分![]() 与
与![]() 交于点
交于点![]() ,当
,当![]() 时,
时,![]() .其中结论正确的有( )
.其中结论正确的有( )
A.2个B.3个C.4个D.5个
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线y=ax2﹣2anx+an2+n+3的顶点P在一条定直线l上.
(1)直接写出直线l的解析式;
(2)对于任意非零实数a,存在确定的n的值,使抛物线与x轴有唯一的公共点,求此时n的值;
(3)当点P在x轴上时,抛物线与直线l的另一个交点Q,过点Q作x轴的平行线,交抛物线于点A,过点Q作y轴的平行线,交x轴于点B,求![]() 的值或取值范围.
的值或取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】综合与探究
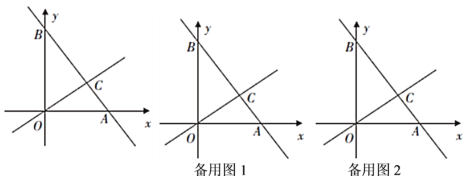
如图,在平面直角坐标系中,直线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() ,且与直线
,且与直线![]() 相交于点
相交于点![]() ,动点
,动点![]() 在
在![]() 轴上运动.
轴上运动.
(1)求直线![]() 的函数表达式;
的函数表达式;
(2)求使![]() 的周长最小时点
的周长最小时点![]() 的坐标;
的坐标;
(3)在![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() 是以
是以![]() 为直角边的直角三角形?如果存在,直接写出点
为直角边的直角三角形?如果存在,直接写出点![]() 的坐标;如果不存在,请说明理由.
的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】列方程(组)解应用题:
汾河古称“汾”,又称汾水,是山西最大的河流,被山西人称为“母亲河”,对山西省的历史文化有着深远的影响.为打造“一川清水、两岸锦绣”的生态环境,现将一段长为![]() 的汾河两岸绿化任务交由甲、乙两个工程队先后接力完成.甲工程队每天绿化
的汾河两岸绿化任务交由甲、乙两个工程队先后接力完成.甲工程队每天绿化![]() ,乙工程队每天绿化
,乙工程队每天绿化![]() ,共用时
,共用时![]() 天.
天.
根据以上信息,小敏和小颖由自己的设想方案分别列出了尚不完整的方程组:
小敏:
小颖: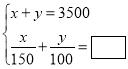

(1)请你在方框中补全小敏和小颖所列的方程组;
(2)根据小敏和小颖所列的方程组,分别指出未知数![]() ,
,![]() 表示的实际意义:
表示的实际意义:
小敏:![]() 表示_____________,
表示_____________,![]() 表示____________;
表示____________;
小颖:![]() 表示____________,
表示____________,![]() 表示______________;
表示______________;
(3)请你选择一种方案,求甲、乙两工程队分别绿化河岸多少米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com