
科目: 来源: 题型:
【题目】某市举行“行动起来,对抗雾霾”为主题的植树活动,某街道积极响应,决定对该街道进行绿化改造,共购进甲、乙两种树共50棵,已知甲树每棵800元,乙树每棵1200元.
(1)若购买两种树的总金额为56000元,求甲、乙两种树各购买了多少棵?
(2)若购买甲树的金额不少于购买乙树的金额,至少应购买甲树多少棵?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,△ABC是等边三角形,△ABD是等腰直角三角形,∠BAD=90°,AE⊥BD于点E,连CD分别交AE,AB于点F,G,过点A作AH⊥CD交BD于点H.则下列结论:①∠ADC=15°;②AF=AG;③AH=DF;④△AFG∽△CBG;⑤AF=(![]() ﹣1)EF.其中正确结论的个数为( )
﹣1)EF.其中正确结论的个数为( )
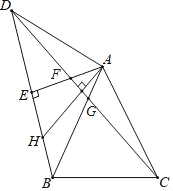
A. 5 B. 4 C. 3 D. 2
查看答案和解析>>
科目: 来源: 题型:
【题目】新华商场销售某种冰箱,每台进货价为2500元.市场调研表明:当销售价为2900元时,平均每天能售出8台;而当销售价每降低50元时,平均每天就能多售出4台.商场要想使这种冰箱的销售利润平均每天达到5000元,设每台冰箱的定价为x元,则x满足的关系式为( )
A. (x2500)(8+4×![]() )=5000 B. (2900x2500)(8+4×
)=5000 B. (2900x2500)(8+4×![]() )=5000
)=5000
C. (x2500)(8+4×![]() )=5000 D. (2900x)(8+4×
)=5000 D. (2900x)(8+4×![]() )=5000
)=5000
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,∠AOB=60°,点P是∠AOB内的定点且OP=![]() ,若点M、N分别是射线OA、OB上异于点O的动点,则△PMN周长的最小值是( )
,若点M、N分别是射线OA、OB上异于点O的动点,则△PMN周长的最小值是( )
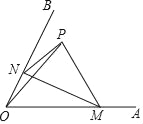
A. ![]() B.
B. ![]() C. 6 D. 3
C. 6 D. 3
查看答案和解析>>
科目: 来源: 题型:
【题目】(1)把下面的证明补充完整
已知:如图,直线AB、CD被直线EF所截,AB∥CD,EG平分∠BEF,FG平分∠DFE,EG、FG交于点G.求证:EG⊥FG.
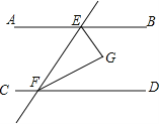
证明:∵AB∥CD(已知)
∴∠BEF+∠DFE=180°(______),
∵EG平分∠BEF,FG平分∠DFE(已知),
∴______,______(______),
∴∠GEF+∠GFE=![]() (∠BEF+∠DFE)(______),
(∠BEF+∠DFE)(______),
∴∠GEF+∠GFE=![]() ×180°=90°(______),
×180°=90°(______),
在△EGF中,∠GEF+∠GFE+∠G=180°(______),
∴∠G=180°-90°=90°(等式性质),
∴EG⊥FG(______).
(2)请用文字语言写出(1)所证命题:______.
查看答案和解析>>
科目: 来源: 题型:
【题目】某日,正在我国南海海域作业的一艘大型渔船突然发生险情,相关部门接到求救信号后,立即调遣一架直升飞机和一艘刚在南海巡航的渔政船前往救援.当飞机到达距离海面3000米的高空C处,测得A处渔政船的俯角为60°,测得B处发生险情渔船的俯角为30°,请问:此时渔政船和渔船相距多远?(结果保留根号)
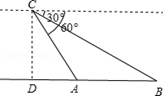
查看答案和解析>>
科目: 来源: 题型:
【题目】 某校为了了解学生的安全意识,在全校范围内随机抽取部分学生进行问卷调查.根据调查结果,把学生的安全意识分成“淡薄”、“一般”、“较强”、“很强”四个层次,并绘制成如下两幅尚不完整的统计图,如图所示:

根据以上信息,解答下列问题:
(1)这次调查一共抽取了______名学生,将条形统计图补充完整;
(2)扇形统计图中,“较强”层次所占圆心角的大小为______°;
(3)若该校有3200名学生,现要对安全意识为“淡薄”、“一般”的学生强化安全教育,根据调查结果,请你估计全校需要强化安全教育的学生人数.
查看答案和解析>>
科目: 来源: 题型:
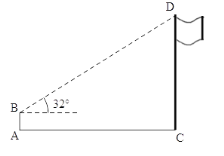
【题目】如图,在数学实践课中,小明为了测量学校旗杆CD的高度,在地面A处放置高度为1.5米的测角仪AB,测得旗杆顶端D的仰角为32°,AC为22米,求旗杆CD的高度.(结果精确到0.1米.参考数据:sin32°= 0.53,cos32°= 0.85,tan32°= 0.62)
查看答案和解析>>
科目: 来源: 题型:
【题目】[建立模型]
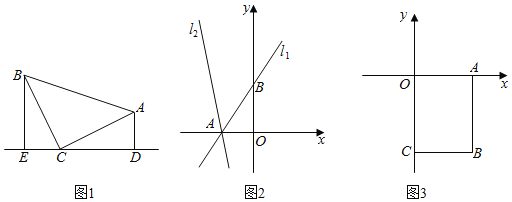
(1)如图1.等腰![]() 中,
中, ![]() ,
, ![]() ,直线
,直线![]() 经过点
经过点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,求证:
,求证: ![]() ;
;
[模型应用]
(2)如图2.已知直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,将直线
,将直线![]() 绕点
绕点![]() 逆时针旋转45'°至直线
逆时针旋转45'°至直线![]() ,求直线
,求直线![]() 的函数表达式:
的函数表达式:
(3)如图3,平面直角坐标系内有一点![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() ,BC⊥y
,BC⊥y![]() 轴于点
轴于点![]() ,点
,点![]() 是线段
是线段![]() 上的动点,点
上的动点,点![]() 是直线
是直线![]() 上的动点且在第四象限内.试探究
上的动点且在第四象限内.试探究![]() 能否成为等腰直角三角形?若能,求出点
能否成为等腰直角三角形?若能,求出点![]() 的坐标,若不能,请说明理由.
的坐标,若不能,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
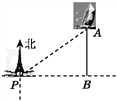
【题目】如图,一艘海轮位于灯塔P的北偏东方向55°,距离灯塔为2海里的点A处.如果海轮沿正南方向航行到灯塔的正东位置,海轮航行的距离AB长是( )
A. 2海里 B. 2sin 55°海里
C. 2cos 55°海里 D. 2tan 55°海里
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com