
科目: 来源: 题型:
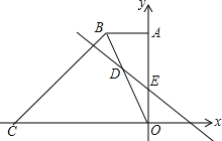
【题目】如图,在平面直角坐标中,直角梯形OABC的边OC、OA分别在x轴、y轴上,AB∥OC,∠AOC=90°,∠BCO=45°,BC=12![]() ,点C的坐标为(-18,0).
,点C的坐标为(-18,0).
(1)求点B的坐标;
(2)若直线DE交梯形对角线BO于点D,交y轴于点E,且OE=4,∠OFE=45°,求直线DE的解析式;
(3)求点D的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】二次函数![]() 的部分图象如图所示,图象过点
的部分图象如图所示,图象过点![]() ,对称轴为直线
,对称轴为直线![]() ,下列结论:
,下列结论: ![]() ;
; ![]() ;
; ![]() ;
; ![]() 若点
若点![]() 、点
、点![]() 、点
、点![]() 在该函数图象上,则
在该函数图象上,则![]() ;
; ![]() 若方程
若方程![]() 的两根为
的两根为![]() 和
和![]() ,且
,且![]() ,则
,则![]() 其中正确的结论是______.
其中正确的结论是______.
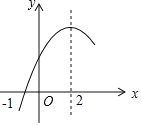
查看答案和解析>>
科目: 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图所示.下列结论:①abc>0;②2a﹣b<0;③4a﹣2b+c<0;④(a+c)2<b2其中正确的个数有( )
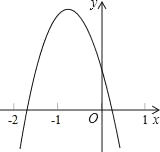
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目: 来源: 题型:
【题目】某工程队承包了某标段全长1755米的过江隧道施工任务,甲、乙两个班组分别从东、西两端同时掘进.已知甲组比乙组平均每天多掘进0.6米,经过5天施工,两组共掘进了45米.
(1)求甲、乙两个班组平均每天各掘进多少米?
(2)为加快工程进度,通过改进施工技术,在剩余的工程中,甲组平均每天能比原来多掘进0.2米,乙组平均每天能比原来多掘进0.3米.按此旄工进度,能够比原来少用多少天完成任务?
查看答案和解析>>
科目: 来源: 题型:
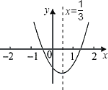
【题目】小明从如图所示的二次函数![]() 的图象中,观察得出了下面五条信息:
的图象中,观察得出了下面五条信息:
①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() ,⑤
,⑤![]() ,
,
你认为其中正确信息的个数有( )
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,在平面直角坐标系中,直线AB与![]() 轴交于点A,与
轴交于点A,与![]() 轴交于点B,与直线OC:
轴交于点B,与直线OC:![]() 交于点C.
交于点C.
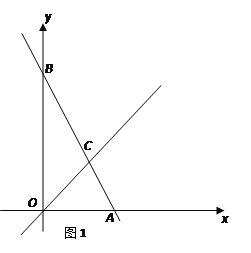

(1)若直线AB解析式为![]() ,
,
①求点C的坐标;
②求△OAC的面积.
(2)如图2,作![]() 的平分线ON,若AB⊥ON,垂足为E, OA=4,P、Q分别为线段OA、OE上的动点,连结AQ与PQ,试探索AQ+PQ是否存在最小值?若存在,求出这个最小值;若不存在,说明理由.
的平分线ON,若AB⊥ON,垂足为E, OA=4,P、Q分别为线段OA、OE上的动点,连结AQ与PQ,试探索AQ+PQ是否存在最小值?若存在,求出这个最小值;若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】(1)如图1,OC平分∠AOB,点P在OC上,若⊙P与OA相切,那么⊙P与OB位置关系是 .
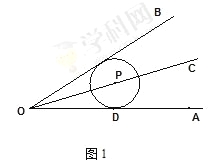
(2)如图2,⊙O的半径为2,∠AOB=120°,
①若点P是⊙O上的一个动点,当PA=PB时,是否存在⊙Q,同时与射线PA.PB相切且与⊙O相切,如果存在,求出⊙Q的半径; 如果不存在,请说明理由.
②若点P在BO的延长线上,且满足PA⊥PB,是否存在⊙Q,同时与射线PA.PB相切且与⊙O相切,如果存在,请直接写出⊙Q的半径; 如果不存在,请说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】联想三角形内心的概念,我们可引入如下概念.
定义:到三角形的两边距离相等的点,叫做此三角形的准内心.
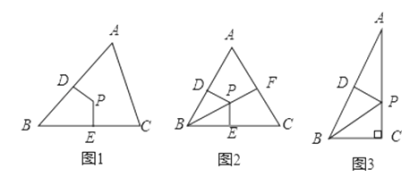
举例:如图1,若PD=PE,则点P为△ABC的准内心.
应用:如图2,BF为等边三角形的角平分线,准内心P在BF上,且PF=![]() BP,求证:点P是△ABC的内心.
BP,求证:点P是△ABC的内心.
探究:已知△ABC为直角三角形,∠C=90°,准内心P在AC上,若PC=![]() AP,求∠A的度数.
AP,求∠A的度数.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,AC是直径,过O作OD∥BC交AB于点D.延长DO交⊙O于点E,作EF⊥AC于点F.连接DF并延长交直线BC于点G,连接EG.
(1)求证:FC=GC;
(2)求证:四边形EDBG是矩形.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com