
科目: 来源: 题型:
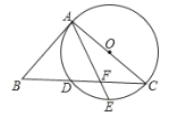
【题目】如图,AC是⊙O的直径,BC交O于点D,E是弧CD的中点,连接AE交BC于点F,∠ABC=2∠EAC.
(1)求证:AB是⊙O的切线;
(2)若 tanB=![]() ,BD=6,求CF的长.
,BD=6,求CF的长.
查看答案和解析>>
科目: 来源: 题型:
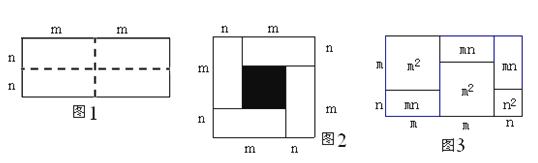
【题目】沿图1长方形中的虚线平均分成四块小长方形,然后按图2的形状拼成一个正方形![]() .
.
(1)图2中的阴影部分的面积为 .
(2)观察图2,请你写出代数式(m+n)2、(m-n)2、mn之间的等量关系式.
(3)根据你得到的关系式解答下列问题:若x+y=-6,xy=5,则x–y= .
(4)实际上有许多代数恒等式可以用图形的面积来表示.如图3,它表示了(2m+n)(m+n)=2m2+3mn+n2.试画出一个几何图形,使它的面积能表示(m+n)(m+3n)=m2+4mn+3n2.
查看答案和解析>>
科目: 来源: 题型:
【题目】某商品交易会上,一商人将每件进价为 5 元的纪念品,按每件 9 元出售,每天可售出 32件.他想采用提高售价的办法来增加利润,经试验,发现这种纪念品每件提价 2 元,每天的销售量会减少 8 件.
(1)当售价定为多少元时,每天的利润为 140 元?
(2)写出每天所得的利润 y(元)与售价 ![]() (元/件)之间的函数关系式,每件售价定为多少元,才能使一天所得的利润最大?最大利润是多少元?(利润=(售价-进价)×售出件数)
(元/件)之间的函数关系式,每件售价定为多少元,才能使一天所得的利润最大?最大利润是多少元?(利润=(售价-进价)×售出件数)
查看答案和解析>>
科目: 来源: 题型:
【题目】已知二次函数y=﹣x2+2x.
(1)在给定的平面直角坐标系中,画出这个函数的图象;
(2)根据图象,写出当y<0时,x的取值范围;
(3)若将此图象沿x轴向左平移3个单位,再沿y轴向下平移1个单位,请直接写出平移后图象所对应的函数关系式.

查看答案和解析>>
科目: 来源: 题型:
【题目】(本题满分8分)一个不透明的口袋中装有2个红球(记为红球1、红球2)、1个白球、1个黑球,这些球除颜色外都相同,将球摇匀.
(1)从中任意摸出1个球,恰好摸到红球的概率是 ;
(2)先从中任意摸出1个球,再从余下的3个球中任意摸出1个球,请用列举法(画树状图或列表)求两次都摸到红球的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点A(1,0),B(1﹣a,0),C(1+a,0)(a>0),点P在以D(4,4)为圆心,1为半径的圆上运动,且始终满足∠BPC=90°,则a的最大值是______.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c交x轴于(﹣1,0)、(3,0)两点,以下四个结论正确的是(用序号表示)______________.
(1)图象的对称轴是直线 x=1
(2)当x>1时,y随x的增大而减小
(3)一元二次方程ax2+bx+c=0的两个根是﹣1和3
(4)当﹣1<x<3时,y<0.
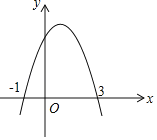
查看答案和解析>>
科目: 来源: 题型:
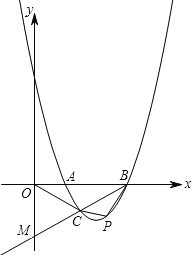
【题目】如图,抛物线y=a(x﹣1)(x﹣3)(a>0)与x轴交于A、B两点,抛物线上另有一点C在x轴下方,且使△OCA∽△OBC.
(1)求线段OC的长度;
(2)设直线BC与y轴交于点M,点C是BM的中点时,求直线BM和抛物线的解析式;
(3)在(2)的条件下,直线BC下方抛物线上是否存在一点P,使得四边形ABPC面积最大?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图:在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,BD=DF,
(1)证明:CF=EB.
(2)证明:AB=AF+2EB.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com