
科目: 来源: 题型:
【题目】(本小题满分10分)如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() (
(![]() 为常数,且
为常数,且![]() )的图象交于A(1,a)、B两点.
)的图象交于A(1,a)、B两点.

(1)求反比例函数的表达式及点B的坐标;
(2)在x轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标及△PAB的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】直角三角形的铁片ABC的两条直角边BC,AC的长分别为3cm和4cm,如图所示分别采用⑴,⑵两种方法,剪去一块正方形铁片,为了使剪去正方形铁片后剩下的边角料较少,试比较哪一种剪法较为合理,并说明理由.
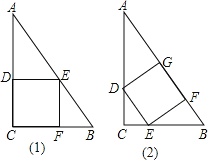
查看答案和解析>>
科目: 来源: 题型:
【题目】(7分)某兴趣小组开展课外活动.如图,A,B两地相距12米,小明从点A出发沿AB方向匀速前进,2秒后到达点D,此时他(CD)在某一灯光下的影长为AD,继续按原速行走2秒到达点F,此时他在同一灯光下的影子仍落在其身后,并测得这个影长为1.2米,然后他将速度提高到原来的1.5倍,再行走2秒到达点H,此时他(GH)在同一灯光下的影长为BH(点C,E,G在一条直线上).
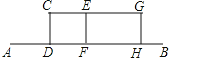
(1)请在图中画出光源O点的位置,并画出他位于点F时在这个灯光下的影长FM(不写画法);
(2)求小明原来的速度.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,一次函数y=mx+b的图象与反比例函数y=![]() 的图象交于A(3,1),B(﹣
的图象交于A(3,1),B(﹣![]() ,n)两点.
,n)两点.
(1)求该反比例函数的解析式;
(2)求n的值及该一次函数的解析式.

查看答案和解析>>
科目: 来源: 题型:
【题目】人们在长期的数学实践中总结了许多解决数学问题的方法,形成了许多光辉的数学想法,其中转化思想是中学教学中最活跃,最实用,也是最重要的数学思想,例如将不规则图形转化为规则图形就是研究图形问题比较常用的一种方法.
问题提出:求边长分别为、![]() 、
、![]() 、
、![]() 的三角形面积.
的三角形面积.
问题解决:
在解答这个问题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出边长分别为
![]() 、
、![]() 、
、![]() 的格点三角形
的格点三角形![]() (如图),
(如图),![]() 是角边为1和2的直角三角形斜边,
是角边为1和2的直角三角形斜边,![]() 是直角边分别为1和3的直角三角形的斜边,
是直角边分别为1和3的直角三角形的斜边,![]() 是直角边分别为2和3的直角三角形斜边,用一个大长方形的面积减去三个直角三角形的面积,这样不需求
是直角边分别为2和3的直角三角形斜边,用一个大长方形的面积减去三个直角三角形的面积,这样不需求![]() 的高,而借用网格就能计算它的面积.
的高,而借用网格就能计算它的面积.
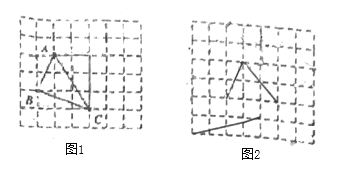
(1)请直接写出图①中![]() 的面积为____________.
的面积为____________.
(2)类比迁移:求边长分别为![]() 、
、![]() 、
、![]() 的三角形面积(请利用图②的正方形网格画出相应的
的三角形面积(请利用图②的正方形网格画出相应的![]() ,并求出它的面积)
,并求出它的面积)
(3)思维拓展:求边长分别为![]() ,的三角形的面积
,的三角形的面积
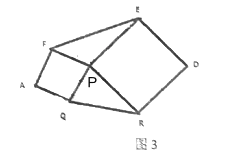
(4)如图(3),已知![]() ,以
,以![]() ,
,![]() 为边向外作正方形
为边向外作正方形![]() ,正方形
,正方形![]() ,连接
,连接![]() ,若
,若![]() ,则六边形
,则六边形 ![]() 的面积是_________.
的面积是_________.
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读下列两段材料,回答问题:
材料一:A(x1.y1),B(x2.y2)的中点坐标为(![]() ,
,![]() ) 例如,点(1,5),(3,-1)的中点坐标为(
) 例如,点(1,5),(3,-1)的中点坐标为(![]() ,
,![]() ),即(2, 2)
),即(2, 2)
材料二:如图1,正比例函数l1:y=k1x和l2:y=k2x的图像相互垂直,分别在l1和l2上取点A、B,使得AO=BO.分别过点A、B作x轴的垂线,垂足分别为点C、D.显然△AOC≌△ OBD.设OC=BD=a,AC=OD=b.则A(-a,b),B(b,a).于是![]() ,所以k1k2的值为一个常数.
,所以k1k2的值为一个常数.
(1)在材料二中,k1k2=____ (写出这个常数具体的值) ;
(2)如图,在矩形OBAC中A(4,2),点D是OA中点,用两段材料的结论,求点D的坐标和OA的垂直平分线l的解析式;
(3)若点C’ 与点C关于OA对称,用两段材料的结论,求点C'的坐标,

查看答案和解析>>
科目: 来源: 题型:
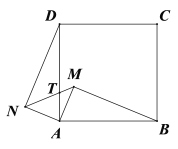
【题目】如图,在Rt△ABM和Rt△ADN的斜边分别为正方形的边AB和AD,其中AM=AN.
(1)求证:Rt△ABM≌Rt△AND
(2)线段MN与线段AD相交于T,若AT=![]() ,求
,求![]() 的值
的值
查看答案和解析>>
科目: 来源: 题型:
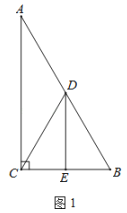
【题目】在Rt△ABC中,∠ACB=90°,∠A=30°,点D是AB的中点,DE⊥BC,垂足为点E,连接CD.
(1)如图1,求DE与BC的数量关系;
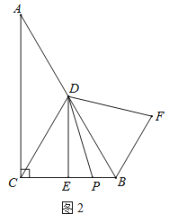
(2)如图2,若P是线段CB上一动点(点P不与点B、C重合),连接DP,将线段DP绕点D逆时针旋转60°,得到线段DF,∠PDF=60°连接BF,请猜想DE、BF、BP三者之间的数量关系,并证明你的结论;
查看答案和解析>>
科目: 来源: 题型:
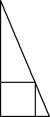
【题目】《九章算术》是我国古代数学名著,书中有下列问题:“今有勾五步,股十二步,问勾中容方几何?”其意思为“今有直角三角形,勾(短直角边)长为5步,股(长直角边)长为12步,问该直角三角形能容纳的正方形边长最大是多少步?”该问题的答案是________步.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com