科目： 来源： 题型：
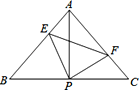
【题目】已知△ABC中，AB=AC，∠BAC=90°，直角∠EPF的顶点P是BC中点，两边PE、PF分别交AB、AC于点E、F，给出的以下四个结论：①AE=CF； ②△EPF一定是等腰直角三角形； ③S四边形AEPF=
S△ABC；④当∠EPF在△ABC内绕顶点P旋转时始终有EF=AP。（点E不与A、B重合），上述结论中始终正确的有_____.（写序号）
查看答案和解析>>
科目： 来源： 题型：
【题目】如图，
与
的平分线相交于点P，
，PB与CE交于点H，
交BC于F，交AB于G，下列结论：①
；②
；③ BP垂直平分CE；④
，其中正确的判断有（ ）
A. ①②B. ③④C. ①③④D. ①②③④
查看答案和解析>>
科目： 来源： 题型：
【题目】如图，等边三角形ABC的边长为4，AD是BC边上的中线，F是AD边上的动点，E是AC边上一点．若AE＝2，当EF＋CF取得最小值时，∠ECF的度数为( )
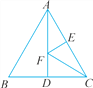
A. 20° B. 25° C. 30° D. 45°
查看答案和解析>>
科目： 来源： 题型：
【题目】为丰富学生课外活动，某校积极开展社团活动，开设的体育社团有：A：篮球，B：排球，C：足球，D：羽毛球，E：乒乓球．学生可根据自己的爱好选择一项，李老师对八年级同学选择体育社团情况进行调查统计，制成了两幅不完整的统计图（如图），则以下结论不正确的是（ ）
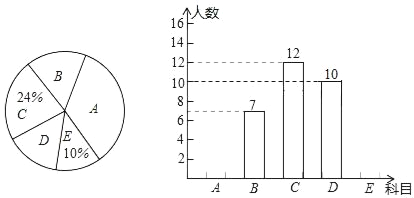
A. 选科目E的有5人
B. 选科目A的扇形圆心角是120°
C. 选科目D的人数占体育社团人数的
D. 据此估计全校1000名八年级同学，选择科目B的有140人
查看答案和解析>>
科目： 来源： 题型：
【题目】已知：如图，在梯形ABCD中，AB∥CD，∠D=90°，AD=CD=2，点E在边AD上（不与点A、D重合），∠CEB=45°，EB与对角线AC相交于点F，设DE=x．
（1）用含x的代数式表示线段CF的长；
（2）如果把△CAE的周长记作C△CAE，△BAF的周长记作C△BAF，设
=y，求y关于x的函数关系式，并写出它的定义域；
（3）当∠ABE的正切值是
时，求AB的长．
查看答案和解析>>
科目： 来源： 题型：
【题目】如图，一次函数y=kx+b（k、b为常数，k≠0）的图象与x轴、y轴分别交于A、B两点，且与反比例函数y=
（n为常数，且n≠0）的图象在第二象限交于点C．CD⊥x轴，垂足为D，若OB=2OA=3OD=12．
（1）求一次函数与反比例函数的解析式；
（2）记两函数图象的另一个交点为E，求△CDE的面积；
（3）直接写出不等式kx+b≤的解集．
查看答案和解析>>
科目： 来源： 题型：
【题目】如图，在△ABC中，AB=AC，△ADE的顶点D，E分别在BC，AC上，且∠DAE=90°，AD=AE．若∠C+∠BAC=145°，则∠EDC的度数为（ ）
A. 17.5° B. 12.5° C. 12° D. 10°
查看答案和解析>>
科目： 来源： 题型：
【题目】如图，△ABC中，∠BAC＝90°，AB＝AC，在△ABC的外侧作直线AP，点C关于直线AP的对称点为点D，连接AD，BD，其中BD交直线AP于点E．
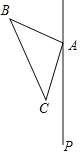
（1）依题意补全图形；
（2）若∠PAC＝24°，求∠AEB的度数；
（3）连结CE，若AE＝
，CE＝1，求BE长．
查看答案和解析>>
科目： 来源： 题型：
【题目】在△ABC中，AB＝17，BC＝21，AC＝10，动点P从点C出发，沿着CB运动，速度为每秒3个单位，到达点B时运动停止，设运动时间为t秒，请解答下列问题：
（1）求BC上的高；
（2）当t为何值时，△ACP为等腰三角形？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
