科目： 来源： 题型：
【题目】如图，在等边三角形ABC中，点D，E分别在边BC，AC上，DE∥AB，过点E作EF⊥DE，交BC的延长线于点F．
（1）求∠F的度数；
（2）若CD＝4，求EF的长．
查看答案和解析>>
科目： 来源： 题型：
【题目】学校需要添置教师办公桌椅A、B两型共200套，已知2套A型桌椅和1套B型桌椅共需2000元，1套A型桌椅和3套B型桌椅共需3000元．
（1）求A，B两型桌椅的单价；
（2）若需要A型桌椅不少于120套，B型桌椅不少于70套，平均每套桌椅需要运费10元．设购买A型桌椅x套时，总费用为y元，求y与x的函数关系式，并直接写出x的取值范围；
（3）求出总费用最少的购置方案．
查看答案和解析>>
科目： 来源： 题型：
【题目】如图，∠A＝∠B＝90°，E是AB上的一点，且AE＝BC，∠1＝∠2．
求证：△CED是等腰直角三角形
证明：∵∠1＝∠2（ ）
∴EC＝ （在一个三角形中，等角对等边）
∵∠A＝∠B＝90°，AE＝BC
∴△AED≌△BCE（ ）
∴∠AED＝∠ （ ）
∵∠BCE+∠BEC＝90°
∠ +∠BEC＝90°（等量代换）
∴∠DEC＝90°．
∴△CED是等腰直角三角形．
查看答案和解析>>
科目： 来源： 题型：
【题目】如图，△ABC是⊙O的内接三角形，AB＝AC，∠BCA＝65°，作CD∥AB，并与○O相交于点D，连接BD，则∠DBC的大小为
A. 15° B. 35° C. 25° D. 45°
查看答案和解析>>
科目： 来源： 题型：
【题目】《九章算术》是我国古代第一部自成体系的数学专著，代表了东方数学的最高成就．它的算法体系至今仍在推动着计算机的发展和应用．书中记载：“今有圆材埋在壁中，不知大小，以锯锯之，深一寸，锯道长一尺，问径几何？”译为：“今有一圆柱形木材，埋在墙壁中，不知其大小，用锯去锯这木材，锯口深1寸（ED=1寸），锯道长1尺（AB=1尺=10寸）”，问这块圆形木材的直径是多少？”
如图所示，请根据所学知识计算：圆形木材的直径AC是（ ）
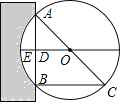
A. 13寸 B. 20寸 C. 26寸 D. 28寸
查看答案和解析>>
科目： 来源： 题型：
【题目】如图，AB是⊙O的直径，PA切⊙O于A，OP交⊙O于C，连接BC．
（Ⅰ）如图①，若∠P=20°，求∠BCO的度数；
（Ⅱ）如图②，过A作弦AD⊥OP于E，连接DC，若OE= 
CD，求∠P的度数．
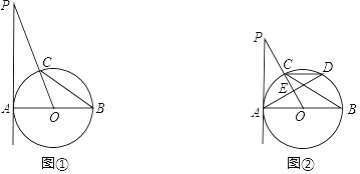
查看答案和解析>>
科目： 来源： 题型：
【题目】我国汉代数学家赵爽为了证明勾股定理，创制了一幅“弦图”，后人称其为“赵爽弦图”（如图（1）所示）．图（2）由弦图变化得到，它是由八个全等的直角三角形拼接而成的记图中正方形ABCD，正方形EFGH，正方形MNKT的面积分别为S1，S2，S3，若EF＝4，则S1+S2+S3的值是（ ）
A.32B.38C.48D.80
查看答案和解析>>
科目： 来源： 题型：
【题目】已知△ABC内接于⊙O，AC是⊙O的直径，D是
的中点．过点D作CB的垂线，分别交CB、CA延长线于点F、E．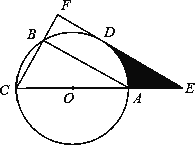 
（1）判断直线EF与⊙O的位置关系，并说明理由；
（2）若CF=6，∠ACB=60°，求阴影部分的面积．
查看答案和解析>>
科目： 来源： 题型：
【题目】在Rt△ABC中，∠C=90°，AC=3，BC=4，AB=5．如图，⊙O是△ABC的内切圆，与三边分别相切于点E、F、G．
（1）求证：内切圆的半径r=1；
（2）求tan∠OAG的值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
