
科目: 来源: 题型:
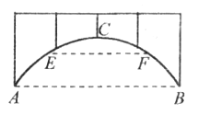
【题目】廊桥是我国古老的文化遗产,如图,是某座抛物线型的廊桥示意图.已知水面AB宽40米,抛物线最高点C到水面AB的距离为10米,为保护廊桥的安全,在该抛物线上距水面AB高为8米的点E,F处要安装两盏警示灯,求这两盏灯的水平距离EF.(结果保留根号)
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:△ABC中,∠ACB=90°,AC=BC.
(1)如图1,点D在BC的延长线上,连AD,过B作BE⊥AD于E,交AC于点F.求证:AD=BF;
(2)如图2,点D在线段BC上,连AD,过A作AE⊥AD,且AE=AD,连BE交AC于F,连DE,问BD与CF有何数量关系,并加以证明;
(3)如图3,点D在CB延长线上,AE=AD且AE⊥AD,连接BE、AC的延长线交BE于点M,若AC=3MC,请直接写出![]() 的值.
的值.

查看答案和解析>>
科目: 来源: 题型:
【题目】小明在学习了如何证明“三边成比例的两个三角形相似”后,运用类似的思路证明了“两角分别相等的两个三角形相似”,以下是具体过程.
已知:如图,在△ABC和△![]() 中,∠A=∠
中,∠A=∠![]() ,∠B=∠
,∠B=∠![]() .
.
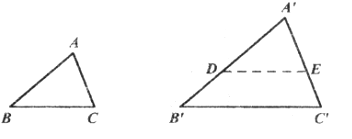
求证:△ABC∽△![]() .
.
证明:在线段![]() 上截取
上截取![]() ,过点D作DE∥
,过点D作DE∥![]() ,交
,交![]() 于点E.
于点E.
由此得到△![]() ∽△
∽△![]() .
.
∴∠![]() =∠
=∠![]() ,
,
∵∠B=∠![]() ,
,
∴∠![]() =∠B,
=∠B,
∵∠![]() =∠A,
=∠A,
∴△![]() ≌△ABC,
≌△ABC,
∴△ABC∽△![]() .
.
小明将证明的基本思路概括如下,请补充完整:
(1)首先,通过作平行线,依据__________,可以判定所作△![]() 与_________;
与_________;
(2)然后,再依据相似三角形的对应角相等和已知条件可以证明所作△![]() 与________;
与________;
(3)最后,可证得△ABC∽△![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】合肥市拟将徽州大道南延至庐江县庐城镇,庐江段的一段土方工程,甲队单独做需40天完成,若乙队先做30天后,甲、乙两队一起合做20天恰好完成任务,请问:
(1)乙队单独做需要多少天才能完成任务?
(2)现将该土方工程分成两部分,甲队做完其中一部分工程用了x天,乙队做完另一部分工程用了y天,若x,y都是正整数,且甲队做的时间不到15天,乙队做的时间不到70天,请用含x的式子表示y,并求出两队实际各做了多少天?
查看答案和解析>>
科目: 来源: 题型:
【题目】如下图,正方形ABCD的边AB在x轴上,A(﹣4,0),B(﹣2,0),定义:若某个抛物线上存在一点P,使得点P到正方形ABCD四个顶点的距离相等,则称这个抛物线为正方形ABCD的“友好抛物线”.若抛物线y=2x2﹣nx﹣n2﹣1是正方形ABCD的“友好抛物线”,则n的值为_____.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,等腰三角形ABC中,AB=AC=4,∠BAC=100°,点D是底边BC的动点(点D不与B、C重合),连接AD,作∠ADE=40°,DE与AC交于点E.
(1)当DC等于多少时,△ABD与△DCE全等?请说明理由;
(2)在点D的运动过程中,△ADE的形状可以是等腰三角形吗?若可以,求出∠BDA的度数;若不可以,请说明理由.

查看答案和解析>>
科目: 来源: 题型:
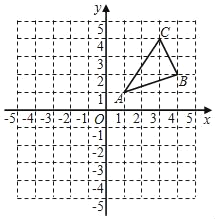
【题目】如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4)
(1)若△A1B1C1与△ABC关于y轴成轴对称,写出△A1B1C1三个顶点坐标:A1= ;B1= ;C1= ;
(2)画出△A1B1C1,并求△A1B1C1面积.
查看答案和解析>>
科目: 来源: 题型:
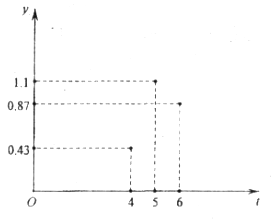
【题目】城市中“打车难”一直是人们关注的一个社会热点问题.近几年来,“互联网+”战略与传统出租车行业深度融合,“优步”、“滴滴出行”等打车软件就是其中典型的应用,名为“数据包络分析”(简称DEA)的一种效率评价方法,可以很好地优化出租车资源配置,为了解出租车资源的“供需匹配”,北京、上海等城市对每天24个时段的DEA值进行调查,调查发现,DEA值越大,说明匹配度越好.在某一段时间内,北京的DEA值y与时刻t的关系近似满足函数关系![]() (a,b,c是常数,且
(a,b,c是常数,且![]() ≠0),如图记录了3个时刻的数据,根据函数模型和所给数据,当“供需匹配”程度最好时,最接近的时刻t是( )
≠0),如图记录了3个时刻的数据,根据函数模型和所给数据,当“供需匹配”程度最好时,最接近的时刻t是( )
A. 4.8 B. 5 C. 5.2 D. 5.5
查看答案和解析>>
科目: 来源: 题型:
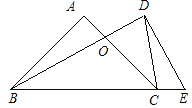
【题目】将一副直角三角板如图摆放,等腰直角三角板ABC的斜边BC与含30°角的直角三角板DBE的直角边BD长度相同,且斜边BC与BE在同一直线上,AC与BD交于点O,连接CD.
求证:△CDO是等腰三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com