练习册

  • 练习册
  • 试题
    相关习题
     0  359739  359747  359753  359757  359763  359765  359769  359775  359777  359783  359789  359793  359795  359799  359805  359807  359813  359817  359819  359823  359825  359829  359831  359833  359834  359835  359837  359838  359839  359841  359843  359847  359849  359853  359855  359859  359865  359867  359873  359877  359879  359883  359889  359895  359897  359903  359907  359909  359915  359919  359925  359933  366461 

    科目： 来源： 题型：

    【题目】数学家吴文俊院士非常重视古代数学家贾宪提出的“从长方形对角线上任一点作两条分别平行于两邻边的直线，则所容两长方形面积相等（如图所示）”这一推论，他从这一推论出发，利用“出入相补”原理复原了《海岛算经》九题古证，根据图形可知他得出的这个推论指（ ）

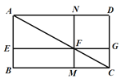
    A. S矩形ABMN＝S矩形MNDCB. S矩形EBMF＝S矩形AEFN

    C. S矩形AEFN＝S矩形MNDCD. S矩形EBMF＝S矩形NFGD

    查看答案和解析>>

    科目： 来源： 题型：

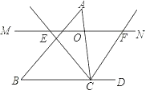
    【题目】如图，△ABC 中，点 O 是边 AC 上一个动点，过 O 作直线 MN∥BC，设 MN 交∠ACB 的平分线于点 E，交∠ACB 的外角平分线于点 F．

    （1）求证：OE＝OF；

    （2）当点 O 在边 AC 上运动到什么位置时，四边形 AECF 是矩形？并说明理由．

    （3）若 AC 边上存在点 O，使四边形 AECF 是正方形，猜想△ABC 的形状并证明你的结论．

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】如图，在△ABC中，AB=AC，以AC为直径的⊙O交BC于点D，交AB于点E，过点D作DF⊥AB，垂足为F，连接DE．

    （1）求证：直线DF与⊙O相切；

    （2）求证：BF=EF；

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】某商品的进价为每件50元．当售价为每件70元时，每星期可卖出300件，现需降价处理，且经市场调查：每降价1元，每星期可多卖出20件．在确保盈利的前提下，解答下列问题：

    （1）若设每件降价x元、每星期售出商品的利润为y元，请写出y与x的函数关系式，并求出自变量x的取值范围；

    （2）当降价多少元时，每星期的利润最大？最大利润是多少？

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】在城镇化建设中，开发商要处理A地大量的建筑垃圾，A地只能容纳1台装卸机作业，装卸机平均每6分钟可以给工程车装满一车建筑垃圾，每辆工程车要将建筑垃圾运送至20千米的B处倾倒，每次倾倒时间约为1分钟，倾倒后立即返回A地等候下一次装运，直到装运完毕；工程车的平均速度为40千米/时．

    （1）一辆工程车运送一趟建筑垃圾（从装车到返回）需要多少分钟？

    （2）至少安排多少辆工程车既能保证装卸机不空闲，又能保证工程车最少等候时间？

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】已知正方形ABCD中，点E在边DC上，DE=2，EC=1(如图所示)把线段AE绕点A旋转，使点E落在直线BC上的点F处，则F、C两点的距离为______．

    查看答案和解析>>

    科目： 来源： 题型：

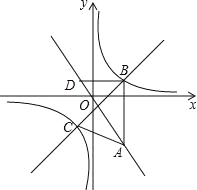
    【题目】如图，在平面直角坐标系xOy中，点A(a，﹣)在直线y＝﹣上，AB∥y轴，且点B的纵坐标为1，双曲线y＝经过点B．

    (1)求a的值及双曲线y＝的解析式；

    (2)经过点B的直线与双曲线y＝的另一个交点为点C，且△ABC的面积为．

    ①求直线BC的解析式；

    ②过点B作BD∥x轴交直线y＝﹣于点D，点P是直线BC上的一个动点．若将△BDP以它的一边为对称轴进行翻折，翻折前后的两个三角形所组成的四边形为正方形，直接写出所有满足条件的点P的坐标．

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】如图，在一个可以自由转动的转盘中，指针位置固定，三个扇形的面积都相等，且分别标有数字1，2，3．

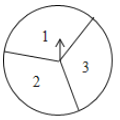
    （1）小明转动转盘一次，当转盘停止转动时，指针所指扇形中的数字是奇数的概率为________；

    （2）小明先转动转盘一次，当转盘停止转动时，记录下指针所指扇形中的数字；接着再转动转盘一次，当转盘停止转动时，再次记录下指针所指扇形中的数字，求这两个数字之和是3的倍数的概率(用画树状图或列表等方法求解)

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】如图，已知，，，且、、三点共线，与交于点．

    （1）求证：；

    （2）若，，则 ．

    查看答案和解析>>

    科目： 来源： 题型：

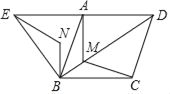
    【题目】如图，四边形ABCD是菱形，AB＝4，且∠ABC＝∠ABE＝60°，M为对角线BD（不含B点）上任意一点，将BM绕点B逆时针旋转60°得到BN，连接EN、AM、CM，则AM+BM+CM的最小值为_____．

    查看答案和解析>>

    同步练习册答案