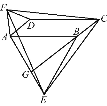
A. 只有①② B. 只有①②③ C. 只有③④ D. ①②③④

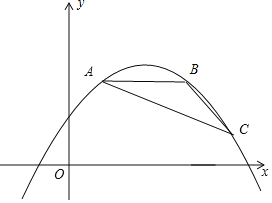
【题目】如图，点A，B，C都在抛物线y=ax2﹣2amx+am2+2m﹣5（其中﹣＜a＜0）上，AB∥x轴，∠ABC=135°，且AB=4．

（1）填空：抛物线的顶点坐标为 （用含m的代数式表示）；

（2）求△ABC的面积（用含a的代数式表示）；

（3）若△ABC的面积为2，当2m﹣5≤x≤2m﹣2时，y的最大值为2，求m的值．

（1）用含x的代数式表示线段CF的长；

（2）如果把△CAE的周长记作C△CAE，△BAF的周长记作C△BAF，设=y，求y关于x的函数关系式，并写出它的定义域；

（3）当∠ABE的正切值是时，求AB的长．

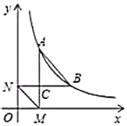
【题目】如图，点、在函数（，且是常数）的图像上，且点在点的左侧过点作轴，垂足为，过点作轴，垂足为，与的交点为，连结、．若和的面积分别为1和4，则的值为（ ）

A.4B.C.D.6

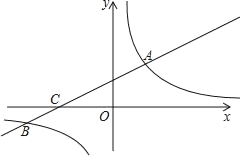
【题目】如图，在平面直角坐标系xOy中，一次函数y=kx+b的图象与反比例函数y=的图象相交于点A（m，3）、B（﹣6，n），与x轴交于点C．

（1）求一次函数y=kx+b的关系式；

（2）结合图象，直接写出满足kx+b＞的x的取值范围；

（3）若点P在x轴上，且S△ACP=S△BOC，求点P的坐标．

【题目】如图是二次函数y=ax2+bx+c图象的一部分，图象过点A（﹣3，0），对称轴为直线x=﹣1，给出以下结论，①ab＜0，②b2﹣4ac＞0，③4b+c＜0，④若B（﹣，y1）、C（﹣，y2）为函数图象上的两点，则y1＞y2，⑤当﹣3≤x≤1时，y≥0，其中正确的结论是（　　）

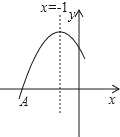
A. 2个 B. 3个 C. 4个 D. 5个

【题目】如图，以平行四边形的边分别做等边和等边．

（1）求证：；

（2）求的度数．

【题目】抛物线，若a，b，c满足b=a+c，则称抛物线为“恒定”抛物线．

（1）求证：“恒定”抛物线必过x轴上的一个定点A；

（2）已知“恒定”抛物线的顶点为P，与x轴另一个交点为B，是否存在以Q为顶点，与x轴另一个交点为C的“恒定”抛物线，使得以PA，CQ为边的四边形是平行四边形？若存在，求出抛物线解析式；若不存在，请说明理由．