
科目: 来源: 题型:
【题目】已知:如图,在四边形ABCD中,AB=CD,AD=BC,点E在CD上,连接AE并延长,交BC的延长线于F.
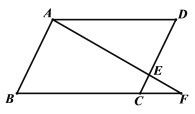
(1)求证:△ADE∽△FCE;
(2)若AB=4,AD=6,CF=2,求DE的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:如图,在菱形ABCD中, BE⊥AD于点E,延长AD至F,使DF=AE,连接CF.

(1)判断四边形EBCF的形状,并证明;
(2)若AF=9,CF=3,求CD的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:如图,在△ABC中,点D在AC上(点D不与A,C重合).若再添加一个条件,就可证出△ABD∽△ACB.
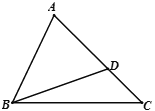
(1)你添加的条件是 ;
(2)根据题目中的条件和添加上的条件证明△ABD∽△ACB.
查看答案和解析>>
科目: 来源: 题型:
【题目】下面是小明设计的“过三角形的一个顶点作该顶点对边的平行线”的尺规作图过程.
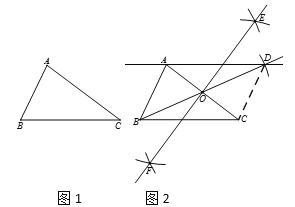
已知:如图1,△ABC.
求作:直线AD,使AD∥BC.
作法:如图2:
①分别以点A、C为圆心,以大于![]() AC为半径作弧,两弧交于点E、F;
AC为半径作弧,两弧交于点E、F;
②作直线EF,交AC于点O;
③作射线BO,在射线BO上截取OD(B与D不重合),使得OD = OB;
④作直线AD.
∴ 直线AD就是所求作的平行线.
根据小明设计的尺规作图过程,完成下面的证明.
证明:连接CD.
∵OA =OC,OB=OD,
∴四边形ABCD是平行四边形(_______________________)(填推理依据).
∴AD∥BC(__________________________________)(填推理依据).
查看答案和解析>>
科目: 来源: 题型:
【题目】某校在“我运动,我快乐”的技能比赛培训活动中,在相同条件下,对甲、乙两名同学的“单手运球”项目进行了5次测试,测试成绩(单位:分)如下:根据右图判断正确的是( )

A.甲成绩的平均分低于乙成绩的平均分;
B.甲成绩的中位数高于乙成绩的中位数;
C.甲成绩的众数高于乙成绩的众数;
D.甲成绩的方差低于乙成绩的方差.
查看答案和解析>>
科目: 来源: 题型:
【题目】瓦子街是上杭城关老城区改造的商业文化购物步行街,瓦子街某商场经营的某个品牌童装,购进时的单价是60元,根据市场调查,在一段时间内,销售单价是80元时,销售量是200件,销售单价每降低1元,就可多售出20件.
![]() 求出销售量
求出销售量![]() 件
件![]() 与销售单价
与销售单价![]() 元
元![]() 之间的函数关系式;
之间的函数关系式;
![]() 求出销售该品牌童装获得的利润
求出销售该品牌童装获得的利润![]() 元
元![]() 与销售单价
与销售单价![]() 元
元![]() 之间的函数关系式;
之间的函数关系式;
![]() 若童装厂规定该品牌童装的销售单价不低于76元且不高于80元,则商场销售该品牌童装获得的最大利润是多少?
若童装厂规定该品牌童装的销售单价不低于76元且不高于80元,则商场销售该品牌童装获得的最大利润是多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】某文具店购进一批纪念册,每本进价为20元,在销售过程中发现该纪念册每周的销售量y(本)与每本纪念册的售价x(元)之间满足一次函数关系:当销售单价为22元时,销售量为36本;当销售单价为24元时,销售量为32本.
(1)求出y与x的函数关系式;
(2)设该文具店每周销售这种纪念册所获得的利润为w元,将该纪念册销售单价定为多少元时,才能使文具店销售该纪念册所获利润最大?最大利润是多少?
查看答案和解析>>
科目: 来源: 题型:
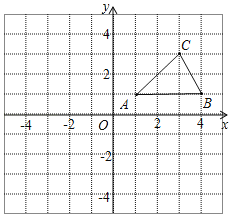
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点坐标分别是A(1,1),B(4,1),C(3,3).
(1)将△ABC向下平移5个单位后得到△A1B1C1,请画出△A1B1C1;
(2)将△ABC绕原点O逆时针旋转90°后得到△A2B2C2,请画出△A2B2C2;
(3)判断以O,A1,B为顶点的三角形的形状.(无须说明理由)
查看答案和解析>>
科目: 来源: 题型:
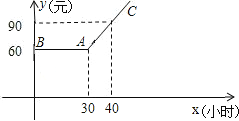
【题目】某市推出电脑上网包月制,每月收取费用y(元)与上网时间x(小时)的函数关系如图所示,其中BA是线段,且BA∥x轴,AC是射线.
(1)当x≥30,求y与x之间的函数关系式;
(2)若小李4月份上网20小时,他应付多少元的上网费用?
(3)若小李5月份上网费用为75元,则他在该月份的上网时间是多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】某企业投资1000万元引进一条农产品生产线,若不计维修、保养费用,预计投产后每年可创330万元,该生产线投产后,从第一年到第x年的维修、保养费用累计为y(万元),且y=ax2+bx(a≠0),若第一年的维修、保养费为20万元,第二年的为40万元.
(1)求y与x之间的函数表达式;
(2)投产后,这个企业在第几年就能收回投资?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com